.JPG)
¡Interpretando lo que leo y comprendiendo lo que escribo!
Armando Rojo (*)
3.Los números naturales
►3.1
CONCEPTO DE NUMERO NATURAL
CONCEPTO DE NUMERO NATURAL
Las expresiones "número natural" y "siguiente de" serán tomadas como términos primitivos. Señalaremos algunas características acerca de ambas.
🔴1° Los números naturales sirven para contar los elementos de cualquier conjunto no infinito.
Representaremos al conjunto de los números naturales mediante N, y escribiremos
Representaremos al conjunto de los números naturales mediante N, y escribiremos
N= { 0, 1, 2, 3, 4, 5, ...}
Como N es infinito no puede ser denotado por extensión. Los puntos suspensivos indican que los elementos de N no se agotan.🔴2° Cada número natural n tiene un único siguiente, que es también natural y denotaremos con s(n). O sea
n ∈ N ⇒ s(n) ∈ N ∧ s(n) es único
Ejemplo 1
s(0) = 1 s(1) = 2
s(8) = 9 s(138) = 139
🔴3° Cada número natural distinto de cero es siguiente de un único número natural. Cero no es siguiente de ningún número natural.
Ejemplo 2
1 es el siguiente de 0.
123 es el siguiente de 122.
🔴4° Supongamos que una cierta propiedad se trasmite de un número a su siguiente. O sea, supongamos que del hecho de que cualquier número n verifique la propiedad se deduce que s(n) también la tiene. Si además el número cero cumple esa propiedad, entonces podemos afirmar que todos los números naturales la verifican.
Para entender mejor lo afirmado, pensemos en una enfermedad de la que sabemos:
- que es hereditaria de padres a hijos en una cierta especie
- que la primera pareja de la especie padeció esa enfermedad.
Podemos afirmar entonces, que toda la especie padece la enfermedad.
En efecto, al tenerla la primera pareja, la heredarán sus hijos, los hijos de sus hijos y así sucesivamente.
En los números naturales sucede lo mismo. Si una característica o propiedad es tal que cada número la hereda del anterior, y el primer número (cero) la posee, entonces todos los números naturales tendrán esa característica o propiedad.
►3.2
REPRESENTACION GRAFICA DE LOS NUMEROS NATURALES
Los números naturales pueden representarse gráficamente mediante puntos equidistantes de una recta, de la siguiente manera:
La representación consiste en asignar a cada número natural un punto de la recta, de modo tal que el siguiente de un número cualquiera se representa a la derecha de éste y entre ambos no se representa ningún otro.
►3.3
NUMEROS PARES E IMPARES
Dos subconjuntos de interés de N son: el de los números pares (P) y el de los números impares (I).
P ={0, 2, 4, 6, 8, ...}
I ={1, 3, 5, 7, 9, ...}
Se verifica que:
🔴1° I y P tienen infinitos elementos.
🔴2º Son disjuntos, pues I ∩ P= ∅.
🔴3º La unión entre ambos es N, o sea, I U P = N.
Entre el conjunto P y el conjunto I es posible establecer una correspondencia o regla que asocie o asigne a cada número par su siguiente.
Gráficamente.
.jpg)
La correspondencia se simboliza con las fechas. Se cumple que:
🔴1° a elementos distintos de P corresponden elementos distintos de I
🔴2° cada elemento de I es el correspondiente de uno de P. Esta situación se describe diciendo que P e I tienen la misma cantidad de elementos (pues corresponde un número impar para cada número par).
Dos conjuntos tienen la misma cantidad de elementos cuando entre ellos es posible establecer una correspondencia que cumpla 1° y 2°.
La noción de cantidad de elementos coincide con la de número de elementos para conjuntos finitos.
En conjuntos infinitos, la noción de cantidad de elementos no es tan intuitiva como muestra el siguiente ejemplo:
Sean
N = { x/x es un número natural}
P= { x/x es un número natural par}
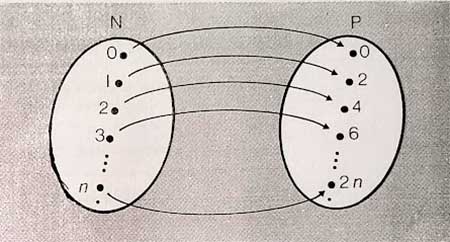
Entonces N y P tienen la misma cantidad de elementos. En efecto, basta considerar la correspondencia que asigna a cada número natural su duplo o doble.
Este hecho puede sorprender, ya que P está estrictamente incluido en N, o sea P⊂ N y P ≠ N.
►3.4
ORDEN EN N
Al contar nombramos a los números naturales en un cierto orden. Comenzamos con el 1, que es el siguiente de 0; continuamos con el 2, que es el siguiente de 1, y así sucesivamente: después de nombrar un número enunciamos el siguiente de dicho número.
Cuando presentamos a los números naturales de este modo decimos que lo hacemos según la sucesión fundamental de los mismos.
Hay una relación asociada a esta sucesión fundamental que es la relación de menor entre números naturales.
Decimos que un número natural a es menor que otro b si en la sucesión fundamental a precede a b.
a<b se lee: a es menor que b.
Introducimos el símbolo ≤ para denotar la relación de menor o igual cuyo significado es el siguiente: 
El símbolo ⟺ se lee si y sólo si y corresponde a una doble implicación, en el sentido siguiente:
La expresión "a > b" se lee: a es mayor que b y se define de la siguiente manera:
Definimos la relación de mayor o igual mediante:
Son verdaderas las siguientes afirmaciones:
2 ≤ 3, 5 ≤ 5, 5 ≥ 5, 7 ≥ 3, 4 > 2
►3.5
PROPIEDADES DE LA RELACION DE MENOR
🔴1° No reflexiva, pues es falso que
a < a
🔴2º No simétrica, ya que
🔴3° Transitiva
Si un número es menor que otro y éste es menor que un tercero, entonces el primero es menor que el tercero.
a < b ∧ b < c ⇒ a < c
La relación de menor es total en el sentido siguiente: dados dos números naturales distintos, uno de ellos es menor que el otro. O sea
a ≠ b ⇒ a < b ∨ b < a
►3.6
PROPIEDADES DE LA RELACION DE MENOR O IGUAL
La relación de menor o igual es:
🔴1° Reflexiva.
∀a ∈ N : a ≤ a
🔴2° Antisimétrica.
a ≤ b ∧ b ≤ a ⇒ a = b
🔴3° Transitiva.
a ≤ b ∧ b ≤ c ⇒ a ≤ c
Ejemplo 1
Hallar la intersección de los conjuntos A y B, siendo
A = { x ∈ N /x ≤7} y B= { x ∈ N / x ≥ 4 }
A∩B = {x ∈ N /x ≤ 7 ∧ x ≥ 4} = { 4 , 5, 6 , 7}
Otra manera de denotar A∩B es
A ∩ B = { x ∈ N / 4 ≤ x ≤ 7}
La notación 4 ≤ x ≤ 7 significa
4 ≤ x ∧ x ≤ 7 o bien
x ≥ 4 ∧ x ≤ 7
Ejemplo 2
Sean A={ x ∈ N / x < 2} y B = { x ∈ N / x ≥ 5 }
Se tiene
A∩B ={ x ∈ N / x < 2 ∧ x ≥ 5} = ∅
A - B = A pues A y B son disjuntos
(A U B)c = {2, 3, 4} = {x ∈ N /2 ≤ x ≤4}
►3.7
NO DENSIDAD DE N
Una propiedad característica del conjunto N ordenado por la relación de menor es la siguiente: entre dos números naturales distintos existe un número finito de naturales.
En virtud de esta propiedad se dice que N no es denso. En cambio, un segmento es un conjunto denso porque entre dos puntos distintos del mismo existen infinitos otros.
►3.8
SISTEMAS DE NUMERACIÓN
Consideremos el conjunto N. Estamos interesados en representar los elementos del mismo.
Como N es infinito, no podemos asignar símbolos independientes a todos los números naturales.
Es posible denotar los números naturales mediante un número finito de símbolos combinándolos de alguna manera preestablecida.
Llamaremos sistema de numeración al conjunto de esos símbolos básicos y las reglas mediante las cuales ellos se vinculan.
Así, cada número natural queda caracterizado por una sucesión de símbolos básicos, que llamaremos, de derecha a izquierda: unidades simples, unidades de primer orden, unidades de segundo orden, y así sucesivamente.
Base del sistema es el número de símbolos básicos.
Por ejemplo, los símbolos básicos del sistema decimal son: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 y su base es diez.
Algunos sistemas de numeración son posicionales en el sentido de que los símbolos básicos, además del valor intrínseco, tienen un valor según la posición que ocupan en la representación del número.
En el sistema decimal una unidad de 1er. orden representa diez unidades simples, una unidad de 2° orden representa diez unidades de ler. orden, y así sucesivamente.
Si la base del sistema es 2, el sistema se llama binario, los símbolos básicos son 0 y 1. En este sistema una unidad de 1er. orden representa 2 unidades simples, y en general una de orden n + 1 representa 2 unidades de orden n.
Ejemplo 1
Determinar cuántas unidades de 2° orden representa una de 5º orden en el sistema binario.
Una unidad de 5° orden representa 2 de 4° orden y cada una de éstas 2 de 3er. orden, y así sucesivamente.
La situación puede representarse mediante el siguiente diagrama:
Luego, una unidad de 5° orden representa 8 unidades de 2° orden.
Ejemplo 2
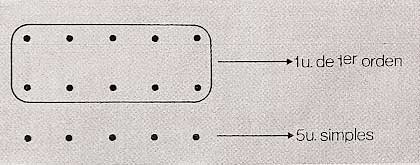
Representamos en el sistema decimal el número quince. Indicaremos con un punto cada unidad simple.
En consecuencia, el número quince se escribe 1510
El subíndice 10 indica la base del sistema. Cuando es 10 se la omite.
Ejemplo 3
Representamos en el sistema binario el número siete.
Entonces siete escrito en el sistema binario es
1112 y se lee: uno uno uno
Ejemplo 4
Representamos el número siete en el sistema de base 3.
Los símbolos básicos del sistema son 0, 1 y 2.
Entonces siete escrito en el sistema de base 3 es 213
Teniendo en cuenta el ejemplo 2, resulta: 1112 = 213
►3.9
NUMERACION ROMANA
En el sistema de numeración romana se emplean los siguientes símbolos:
I, V, X, L, C, D, M (1)
No se aprovecha la posición de los mismos como en el sistema decimal. Es un sistema aditivo, pues simplemente se suman o restan los valores de los símbolos. Dichos valores son:
I → 1
V → 5
X → 10
L → 50
C →100
D → 500
M → 1000
Estos símbolos se utilizan de acuerdo con las siguientes reglas:
🔴1° Un mismo símbolo no se puede repetir en forma consecutiva más de 3 veces.
🔴2° Los símbolos V, L y D no se repiten.
🔴3° Un símbolo que figura a la izquierda de otro mayor se resta; en caso contrario se suma.
🔴4° Los símbolos V, L y D no se anteponen a ninguno mayor.
🔴5° Los símbolos I, X y C sólo pueden figurar a la izquierda de los dos que le siguen en (1). O sea: I puede figurar sólo a la izquierda de V y X .
🔴6° No se puede restar más que un símbolo de cada clase.
🔴7 ° Un trazo horizontal escrito sobre cualquier combinación de símbolos multiplica al número correspondiente por 1.000.
IL es incorrecto, pues contradice la regla 5ª. El número 49 se escribe XLIX.
DM es incorrecto, pues contradice la regla 4°.
Trabajo práctico
3.1 Determinar x en las siguientes igualdades:
1° s(4) = x 4° s (s(2)) = x
2° s (x) = 4 5° s (x + 3) = 5
3° s (s(x)) = 2 6°s (7) = x + 2
3.2 Determinar la relación que vincula a los números naturales a y b en los siguientes casos:
1° a ≥ c ∧ c = d ∧ b < d
2º b = c ∧ a ≤ d ∧ d ≤ c
3.3 Sean A = { x/x ∈ N ∧ x > 2} y
B ={ x/x ∈ N ∧ 1 < x ≤ 10}
Representar gráficamente (en una recta) A - B, B - A y A ∩ B.
3.4 Representar en la recta Ac, siendo
A = {x/x ∈ N / x < 3 ∨ x > 6}
3.5 Demostrar que N tiene la misma cantidad de elementos que I.
3.6 Demostrar que N tiene la misma cantidad de elementos que
{ x/x ∈ N ∧ x ≥ 10 }
3.7 Sea el conjunto A= {1, 2, 3}. Denotar por extensión el conjunto de los números naturales formados por dos cifras de A.
3.8 Indicar qué numero natural es x sabiendo que el punto de la recta que representa a x es el punto medio del segmento que tiene por extremos el punto que representa al número 2 y el punto que representa al siguiente de 7.
3.9 Escribir el mayor de los números de 3 cifras. ¿Cuál es dicho número si las 3 cifras son distintas?
3.10 Determinar el número de unidades de ler. orden que representa una unidad de 3er. orden en el sistema decimal, en el binario y en el cuaternario.
3.11 Escribir en notación decimal
214 , 213 , 1102 ,
3004 , 1013
3.12 Escribir en notación binaria
8 , 9 , 11 , 15.
3.13 Escribir en sistema decimal
3.14 Escribir en notación romana
7.077, 23.050.051, 14, 199.999.
Soluciones3.1 1° 5 2° 3
3° 0 4° 4
5° 1 6º 6
3.2 1° a > b 2° a ≤ b
3.3
3.4
3.5 Consideramos la correspondencia que asigna a cada número natural n el natural 2n + 1.
3.6 Consideramos la correspondencia que asigna a cada número natural n el natural 2n + 10.
3.7 {11, 12, 13, 21, 22, 23, 31, 32, 33 }
3.8 5
3.9 999, 987
3.10 100, 4, 16
3.11 9, 7, 6, 48, 10
3,12 10002 , 10012 ,
10112 , 11112.
3.14 
Tomado de Rojo, A.O. ;Sánchez, S.C. y Greco, M.(1973). Matemática 1. Buenos Aires: El Ateneo.
_______________________
(*)Armando O. Rojo: Profesor de Matemática y Máster en Estadística Matemática. A sido profesor por concurso en las Facultades de Ingeniería y de Ciencias Económicas de la Universidad de Buenos Aires, en el Instituto Nacional Superior del Profesorado y en el Colegio Nacional de Buenos Aires . Así mismo, a dictado cursos de Métodos Cuantitativos para la Toma de Decisiones en el Instituto para el Desarrollo de Empresarios Argentinos. Su labor es bastamente conocida no sólo como docente, sino como autor de obras de Matemática.
Comentarios
Publicar un comentario