¡Interpretando lo que leo y comprendiendo lo que escribo!
Armando Rojo (*)
1.7
ESPACIO Y FIGURAS GEOMÉTRICAS
En el desarrollo de los temas anteriores, las palabras "conjunto" y "elemento" han sido consideradas términos primitivos. En geometría los términos primitivos son: "espacio", "plano", "recta" y "punto".
Los términos primitivos no se definen explícitamente, pero quedan caracterizados por ciertas propiedades que deben satisfacer. Estas propiedades reciben el nombre de axiomas o postulados.
El conjunto universal de la geometría es el espacio E, y sus elementos se llaman puntos. Todo subconjunto del espacio se llama figura. Rectas y planos son subconjuntos del espacio, o sea, figuras.
Daremos algunas aclaraciones intuitivas acerca de los términos primitivos.
🔴 1° A los puntos los designaremos con letras mayúsculas y los representaremos de la siguiente manera:
punto A
La marca "." representa al punto A. Dicha marca no es un punto, pues un punto es mucho más chico que esa y cualquier otra marca que podamos hacer. Un punto no tiene dimensión.
🔴 2° A las rectas las denotaremos en general con letras minúsculas y las representaremos así:
recta r
El trazo ( ╱ ) representa a la recta r, aunque dicho trazo no es una recta. Una recta es más delgada y más larga que cualquier trazo que dibujemos. Una recta tiene una sola dimensión (el largo) respecto de la cual no tiene límites, no termina.
Las rectas son conjuntos infinitos de puntos. Entre dos puntos cualesquiera de una recta, por próximos que estén, siempre hay puntos que pertenecen a la recta, puntos que llenan todo ese trozo de recta. Esto último se sintetiza al decir que la recta es una figura continua. Las rectas no doblan.
🔴 3° Los planos serán denotados con letras griegas y se representarán de la siguiente manera:
plano α
El dibujo no es un plano, porque un plano es más extenso que ese o cualquier otro dibujo que hagamos. Un plano tiene dos dimensiones: el largo y el ancho (en las cuales no posee límites) pero carece de espesor.
Un plano es también un conjunto infinito de puntos, lleno o continuo. Los planos no se curvan.
Ejemplo
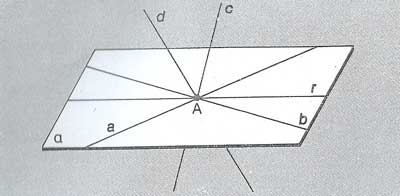
Consideremos el siguiente gráfico:
Se verifica
A, B, C, M, N y P son elementos de E
α ⊂ E, r ⊂ E, s ⊂ E
r ⊂ α , s ⊄ α
A, B, C y P pertenecen a α
Μ ∉ α, Ν ∉ α
A ∈ r, B ∉ s, P ∈ s, P∉ r
1.7
AXIOMAS O POSTULADOS CARACTERÍSTICOS
🔴 A1. Dos puntos distintos pertenecen a una única recta.
La recta r está determinada por los puntos A y B, razón por la cual se la llama recta AB y se la simboliza AB, o sea
r = AB.
Si A y B representan el mismo punto, por él pasan infinitas rectas.
Tres puntos pertenecientes a una misma recta se dicen alineados.
🔴 A2. Una recta y un punto no perteneciente a la misma caracterizan un único plano.
El plano α está determinado por la recta r y el punto P. Si P ∈ r, entonces por r y P pasan infinitos planos:
🔴 A3. La recta determinada por dos puntos distintos de un plano está incluida en dicho plano.
A ∈ α, B ∈ α y A ≠ B ⇒ AB ⊂ α
Oportunamente enunciaremos otros postulados.
1.9
SEMIRRECTA, SEMIPLANO Y SEMIESPACIO
Todo punto de una recta determina dos figuras llamadas semirrectas.
El único punto de r que pertenece a las dos semirrectas es O, y se llama origen de las mismas.
Para denotar una semirrecta se elige un punto A de la misma, distinto del origen y se escribe:
símbolos que se leen: semirrecta de origen O que pasa por A.
Si de una semirrecta se excluye el origen, la figura que se obtiene se llama semirrecta abierta.
Se verifica
O ∈ S (O,A)
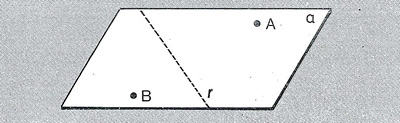
Análogamente, toda recta incluida en un plano determina dos semiplanos opuestos.
S [r, A) se lee: semiplano de borde r que pasa por A
S (r, A) es el semiplano abierto de borde r que pasa por A.
r ⊂ S [ r, A) y r ⊄ ( r, A)
Todo plano determina dos semiespacios opuestos
S [α,B) se lee: semiespacio de borde α que pasa por B.
Tomado de: Rojo, A. O.; Sánchez, S.C. y Greco, M. (1973). Matemática 1. Buenos Aires: El Ateneo.
_________________________
(*)Armando O. Rojo: Profesor de Matemática y Máster en Estadística Matemática. A sido profesor por concurso en las Facultades de Ingeniería y de Ciencias Económicas de la Universidad de Buenos Aires, en el Instituto Nacional Superior del Profesorado y en el Colegio Nacional de Buenos Aires . Así mismo, a dictado cursos de Métodos Cuantitativos para la Toma de Decisiones en el Instituto para el Desarrollo de Empresarios Argentinos. Su labor es bastamente conocida no sólo como docente, sino como autor de obras de Matemática.
 Te recomendamos leer :
Te recomendamos leer :


















Comentarios
Publicar un comentario