En esta publicación continuamos transcribiendo parte de los juegos avanzados que figuran en el libro de Siegfried Kothe, (1991), Cómo utilizar los Bloques LÓGICOS de Z. P. Dienes. Barcelona: TEIDE.
Te recomendamos leer previamente:
II JUEGOS AVANZADOS
(Continuación)
3 JUEGOS DE TRANSFORMACIÓN
Los juegos pueden diversificarse aún más al introducir una nueva operación, que simbolizaremos con una flecha. Plantearemos a los niños un juego de equipo lleno de atractivo. Estos juegos no exigen un gran esfuerzo intelectual. Sin embargo. suponen unas formas de relación social muy concretas que no presentan otra clase de problemas distintos de los que se plantean con un niño.
El trabajo en equipo requiere la atención del profesor en cuanto a la formación de los equipos y su funcionamiento. Las discusiones son frecuentes.
Como es lógico, son importantes las diferencias que surgen cuando uno o varios, aparentemente, no han observado alguna de las reglas del juego. A los mismos adultos nos cuesta a veces escuchar con calma el argumento de un interlocutor, para luego estar de acuerdo o rechazarlo con una serie lógica de contra argumentos. Subrayamos la importancia de la posibilidad de educación social aquí señalada, puesto que pasaremos a exponer juegos en los que siempre participan dos niños. Si en una mesa surge desacuerdo, el profesor no debe intervenir de inmediato. Si deseamos enseñar a discutir con objetividad, no podemos intervenir a base de imponer calma con una orden, sino que debemos encauzar a los contendientes hacia un acuerdo aceptado por ambos,
Juego 40
Repartimos equitativamente
En el primer juego en equipos de dos cada niño debe tener el mismo número de bloques.(1) ¿Por qué atributo debemos guiarnos para repartirlos? Es posible que los niños den con las respuestas: «Tamaño o grosor». Al introducir cada juego, no nos limitaremos a enunciar las reglas, sino que desarrollaremos la problemática. Además es posible comparar la magnitud de los conjuntos. Cada vez que Ana toma un bloque grueso, Carlos toma uno delgado. Esta distribución es completamente equitativa. Por otra parte, se trata del primer juego de la nueva serie. Los bloques deben dejarse formando dos filas, como indica la figura 45.
Si los niños deseasen distribuir conforme al color, repartiremos los bloques de esta forma: Ana toma todos los bloques rojos, Carlos todos los azules. Los ponemos en fila. Cuando Ana coloca el último bloque rojo, a Carlos también le queda sólo un bloque azul. ¿Qué hacemos con los bloques amarillos? Los dos niños van tomando un bloque cada vez hasta completar la fila. La distribución es exacta. Es decir que podemos repartir los bloques con exactitud, ordenándolos de esta forma (exactamente uno frente a otro). Para repartir equitativamente no es preciso contar. Naturalmente, lo permitiremos cuando los niños deseen mostrar su competencia. El que no sepa contar, determinará si cada uno tiene el mismo número de bloques por medio de la correspondencia biunívoca. Así se denomina el concepto
matemático. «Si tomo los bloques redondos y triangulares y tú te quedas con el resto, los dos tendremos la misma cantidad de bloques, podría decir Ana. El número 24 indica la magnitud del conjunto de bloques que tiene Ana. Carlos se queda con el con-junto diferencia de bloques. Este conjunto también presenta la propiedad 24. Los números son propiedades de los conjuntos. Los bloques del mismo color constituyen un conjunto. Cada uno
de los tres conjuntos presenta la propiedad 16. Los juegos de transformación servirán para practicar esta correspondencia biunívoca. Cada vez cambiaremos el nombre a esta forma de ordenar.
___________________
(1) Generalmente, los niños tienen una idea previa de lo que significa el mismo números. Este concepto deberá desarrollarse ahora.
Juego 41
Reproducir exactamente una fila de bloques
El juego 40 está pensado como preparación para este nuevo juego. En tanto que allí hacíamos corresponder un bloque con otro, sin tener en cuenta sus atributos, en el juego 41 los bloques situados uno frente a otro deben tener tres atributos iguales. Si los repartimos según el tamaño, cada jugador tendrá 24 bloques. El único atributo distinto será el tamaño.
Supongamos que Ana y Carlos siguen jugando juntos. Ana tiene los bloques grandes y Carlos los pequeños. Un niño va formando la fila y el otro la reproduce, después se invierten los papeles. En la figura 46 vemos la fila que Ana ha formado a su gusto. Carlos debe hacer coincidir el color, la forma y el grosor, bloque por bloque. Ana controla que Carlos no se equivoque. ¿Y si Ana no advierte algún error? Todo quedará claro al finalizar el juego. ¿Cómo es posible?
Muy pocos niños podrán plantearse mentalmente este problema. Al principio, el esfuerzo resulta excesivo para la mayoría. Si el lector no conoce el juego, puede intentar comprobar si está en condiciones de anticipar mentalmente todas las posibilidades del juego. Resulta sorprendente comprobar la práctica que en ello adquieren los niños. La pregunta aún sin contestar nos servirá de ejemplo para señalar la posibilidad de exigir a los niños esfuerzos de razonamiento de este tipo. La inteligencia del niño sólo se desarrolla en los aspectos que reciben un constante estímulo. Con mucha paciencia e intuición también estaremos en condiciones de ayudar a los niños que, por el motivo que fuere, hasta entonces no hayan recibido estímulos suficientes.
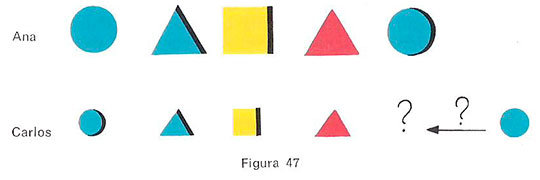
El juego 41 posee un interesante efecto autorrectificador. Si a Ana le pasa por alto un error de Carlos, en otro punto de la fila éste no logrará encontrar el bloque requerido (del mismo color, forma y grosor) en el conjunto residual. La reacción de los adultos cuando los niños identifican un problema pero no logran resolverlo tiene extraordinaria importancia desde el punto de vista pedagógico. Ayudarles a resolverlo sólo tiene un valor educativo cuando lo que se hace es encauzar correctamente la actividad del niño. En la figura 47 tenemos un ejemplo de la situación problemática aquí discutida.
Carlos encuentra un solo bloque redondo que es azul pero no es grueso, en el conjunto residual. ¿Qué debe hacer? ¿Preguntar a los mayores? ¿Reflexionar solo? La pregunta clave es: ¿Dónde hay bloques redondos y azules? Sólo debe comprobarse ese punto. El que vaya comprobando toda la fila bloque por bloque no ha reflexionado bien. Se ha cometido un error en el primer par (2) (fig. 47).
___________________
(2) El pedagogo comprende en qué momentos el niño precisa su ayuda, porque conoce y tiene en cuenta todas estas posibilidades de la educación de la razón. Pero el que tiene que ocuparse simultáneamente de 50 niños se ve desbordado. Los profesores de primer curso sólo pueden tener en cuenta estos detalles cuando los niños trabajan en equipo. Los juegos con los bloques lógicos permiten el trabajo en equipos de acuerdo con los distintos grados de capacidad.
Juego 42
Cambio de atributos entre las filas de bloques
Se pasará a practicar juegos de reproducción en los que se trata de realizar ciertos cambios de atributos. En el juego 41 la distribución de los bloques ha determinado el cambio de un solo atributo. Ahora este cambio de atributo se enunciará expresamente como regla del juego. A fin de simbolizar el cambio requeriremos cartulinas rotuladas con una flecha. Las figuras 48 a, b y c deben interpretarse de la siguiente forma:
figura 48 (a) Cuando un jugador coloca un bloque azul, el otro debe colocar un bloque rojo.
figura 48 (b) Cuando se han colocado bloques rojos, en la otra fila se reproducirá con bloques azules.
figura 48 (c) Emplearemos menos cartulinas si simbolizamos de la forma indicada en esta figura.
Puesto que no se nos dice nada respecto al color amarillo, no lo cambiaremos. Pero primero jugaremos sólo con los bloques no-amarillos (que por tanto son rojos o azules).
Los repartimos de nuevo entre dos niños según el grosor o el tamaño y prescindimos de los bloques amarillos. Al formar estas filas debe prestarse más atención que en el juego 41. En la figura 49 puede verse una de las formas en que podría comenzar el juego. Se han repartido los bloques según el grosor. Empieza Carlos, y Ana va cambiando los colores según lo indicado, pero al mismo tiempo procura hacer coincidir el tamaño y la forma. Introducimos variaciones, pidiendo otros cambios de color.
Juego 43
Se cambian todos los colores
Aumentamos el grado de dificultad. Deben cambiarse los colores de forma cíclica. Se juega con los 48 bloques. Seis cartulinas ( fig.50) indican lo que se debe hacer. En vez de colocar los bloques en fila, también podemos hacer pilas. Pero siempre debe efectuarse el cambio de color requerido, bloque por bloque. El que forma la fila puede seleccionar los bloques según guste. Sólo debe controlar que el compañero de juego reproduzca la fila correctamente, con los cambios indicados. Si se reparten los bloques según el grosor, el tamaño y la forma deben ser iguales. La figura 51 representa el posible desarrollo del juego 43.
Naturalmente aquí también se corrigen los errores, al faltar bloques adecuados a medida que se va desarrollando el juego. Resulta algo más complicado buscar el bloque mal colocado.
Juego 44
Se cambian todas las formas
Aquí se cambian todas las formas según indica la figura 52. Se emplean ocho cartulinas. Repartimos los bloques entre dos jugadores ateniéndonos al tamaño o el grosor. En la figura 53 se ha repartido según el tamaño. También podemos ver el comienzo del juego. Se reproduce el color y grosor.
Juego 45
Jugamos con todas las formas, pero sólo cambiamos algunas de ellas
Las cartulinas indican al niño lo que debe hacer. Jugamos con todos los bloques, repartidos según el grosor. Sólo debe efectuarse el cambio que indica la figura 54, es decir, que no hay nada establecido en cuanto a los bloques redondos y triangulares. ¿Qué hacer? Estas formas no se varían. Por tanto, ahora deben dejarse constantes algunas formas y cambiar otras. En la figura 55 puede verse el comienzo del juego.
Deberían variarse constantemente las reglas de cambio de atributo de los juegos 42 al 45. Para asociar partes de bloques se requiere una concentración intelectual en las normas formales de la correspondencia de atributos. La práctica de esta actividad intelectual particular prepara al niño para aplicarla a problemas matemáticos elementales, una disposición que no puede adquirirse por los procedimientos corrientes de enseñanza del cálculo tradicional. También tiene importancia el cultivo de una comprensión global de los símbolos.
Juego 46
Combinar varios cambios de atributos
En este juego se emplean dos cajas de bloques lógicos. Si cada uno de los dos jugadores dispone de 48 bloques, las exigencias del juego pueden ampliarse de modo considerable. Algunos niños desean que se vayan aumentando las dificultades de esta forma. En la figura 56 puede verse el cambio de todos los atributos que se pide.
La figura 57 representa el comienzo del juego. No se puede exigir a todos los niños el esfuerzo de concentración que se requiere para tener en cuenta simultáneamente el cambio de forma, color, tamaño y grosor.
Juego 47
Algunos bloques están mal colocados. ¿Quién sabe encontrarlos?
Deliberadamente, se colocan algunos bloques en el lugar que no les corresponde, según las reglas de ordenación establecidas.
Los jugadores permanecen en sus sitios y otro niño se acerca a la mesa a investigar cuáles son los bloques mal colocados. Las cartulinas indican los cambios de características que debían efectuarse. El «detective» comprueba donde no se ha cambiado.
Juego 48
¿Quién descubre las reglas del cambio de atributos?
Deberían aprovecharse todas las oportunidades de invertir el desarrollo de los juegos. En los juegos 42-46, ello permite estimular enormemente la agilidad intelectual. Si se juega en varias mesas a la vez, podremos comparar las dos filas de bloques entre las que se ha establecido la correspondencia, y las reglas de transformación simbolizadas por las cartulinas que los mismos niños van variando. Después de comprobar con ayuda de los niños que no se hayan cometido errores, retiraremos las cartulinas sin tocar las filas de bloques. Los niños cambian de mesa e intentan descubrir por observación las reglas de correspondencia adecuadas para cada ordenación de bloques.
Los pequeños siguen diversos procedimientos. No todos los niños son capaces de resolver este enigma. Si alguno pregunta qué debe hacer para descubrir las reglas de correspondencia, ello indica que aún no le hemos dado la preparación deseada para resolver problemas. La independencia intelectual se manifiesta. precisamente en la utilización de todas las experiencias anteriores que permiten resolver el enigma. Supongamos que los bloques se encuentran dispuestos como muestra la figura 58.
No debemos esperar que los niños ya empleen esta estrategia en los primeros intentos de resolver el problema. Es resultado de un proceso de aprendizaje. El profesor no debe «apuntársela» al niño en modo alguno. En la medida de lo posible, el niño debe ir descubriendo las cosas por sí mismo y el profesor sólo debe ayudar en el sentido de impulsar las ideas de aquél. Repetiremos los juegos, a fin de reactivar antiguas experiencias de importancia para la resolución de problemas. Cuando se explica algo se mueven los bloques de la forma correspondiente. Para muchos niños, la explicación verbal que no va acompañada de una acción simultánea con resultados visibles no tiene ningún valor informativo o apenas. En cuanto decae el interés, debe pasarse a practicar juegos conocidos. Los niños siempre deben tener oportunidad de realizar satisfactoriamente los juegos, ya que una serie de fracasos hace flaquear la capacidad de esfuerzo del niño. En este sentido, la pedagogía práctica es un arte que sólo puede aprenderse a través de situaciones reales. El dominio del mismo se manifiesta, por ejemplo, en la forma de diferenciar lo que puede exigirse a cada niño.
Juego 49
¿Quién ha colocado los bloques libremente
y quién los ha ido colocando según las reglas?
Este es un problema difícil que puede plantearse a los niños que no han tenido dificultades en el juego 48. Observamos las dos filas de bloques de la figura 59, entre los que existe una correspondencia.
correspondencia. Sabemos cuál es la fila de Ana y cuál la de Carlos. ¿Pero quién ha colocado los bloques primero y quién los ha ido colocando luego? Podríamos preguntárselo a Carlos, pero no lo quiere decir. No existe, con estos datos, una respuesta absoluta. No podemos decir si ha sido Carlos o ha sido Ana quien ha empezado. Pero puede darse una respuesta condicional, que descubren algunos niños al cabo de cierto tiempo. Si ha comenzado Ana, el azul se cambia por el rojo, pero si ha comenzado Carlos, se cambiará el rojo por el azul. Al enunciarlos, se van señalando los bloques o se colocan las correspondientes cartulinas de colores y las flechas. La utilización de la frase de la forma «si... entonces...» presupone la comprensión de una relación lógica, que denominamos implicación. Es perfectamente posible que los niños descubran esta relación de forma espontánea, a partir de las experiencias adquiridas en los juegos. Tal vez al principio no empleen esas palabras, pero pronto las adoptan, puesto que la relación lógica les es familiar. La manipulación de los bloques lógicos eleva el nivel de razonamiento y ello exige a su vez expresiones lingüísticas diferenciadas. La forma gramatical «si... entonces...» sirve para descubrir los dos cambios de colores posibles que corresponden al supuesto «ha comenzado Ana» o «ha comenzado Carlos». Este complicado problema se pondrá al alcance de muchos niños a través de juegos más sencillos. También puede descubrirse el concepto geométrico de sentido de giro que interviene aquí, el cual además ya aparecía en el juego 13. Repetiremos otros juegos de este tipo y los relacionaremos con el movimiento de las manecillas de un reloj.
Juego 50
¿A quién le toca jugar ahora?
Tres niños se sientan alrededor de una mesa y tienen ante si bloques de un mismo color, El cuarto niño no debe ver como los niños van colocando los bloques por turno, formando una serpiente de colores. Se interrumpe el juego y el cuarto niño debe decir, primero, a quién le toca jugar y luego caminar en torno a la mesa, siguiendo la dirección de los turnos del juego. Por tanto, existen dos direcciones de giro, según puede experimentarse en el juego 50, después de la primera experiencia adquirida en el juego 13.
¿En qué dirección se mueven las manecillas de un reloj? Ponemos un reloj sobre la mesa y observamos el sentido de giro. El que lo identifique debe correr alrededor de la mesa en esa dirección. El juego 50 requiere que se establezca la relación con el sentido de las manecillas del reloj. Si corremos en el sentido de las manecillas del reloj, levantaremos los brazos. Los brazos deben evocar las manecillas, Si corremos en sentido contrario al de las manecillas del reloj, mantendremos los brazos caídos.
Hasta aquí, hemos aplicado las reglas de transformación a la correspondencia entre pares de bloques; ahora se transformarán figuras completas, o sea, un grupo de bloques. Con ello se adquieren experiencias básicas de geometría, que podrán utilizarse más adelante.
Juego 51
El juego de las locomotoras
Con seis bloques azules formamos una locomotora, según muestra la figura 62. Ahora se pide el cambio de color. Tendremos dos locomotoras, una roja, otra amarilla, en las que coincide la forma, tamaño y grosor de todos los bloques, Debe indicarse el cambio de color por medio de cartulinas.
Puede variarse el juego, partiendo de otras figuras. Pueden transformarse, por ejemplo, las formas obtenidas en la figura 1.
Juego 52
Comparamos las locomotoras
Si además del color se varía el grosor, las transformaciones tampoco tienen gran importancia. No debemos olvidarnos de indicar con cartulinas las reglas de cambio de atributos. Cuando se varía el tamaño, la locomotora transformada tiene una forma curiosa (fig. 63), La chimenea está flotando en el aire. Las ruedas son más grandes que el cuerpo de la locomotora.
Es posible que se establezcan ciertas asociaciones. En las ferias hay unos curiosos espejos, que transforman al observador de una forma muy divertida. Se trata de valiosas experiencias primarias, que más adelante se estudiarán sistemáticamente en clase de geometría. Entonces se dirá, por ejemplo, que «la elipse es la figura afín al círculo».
En el juego 52 deben compararse, sobre todo, distintas locomotoras transformadas, entre sí y con la locomotora original. Se trata de identificar a través de ello el cambio de atributos y simbolizarlo con cartulinas. También se pregunta cómo podrían invertirse las transformaciones. Una sola caja de bloques lógicos no permite dar rienda suelta a la fantasía, ya que no es posible efectuar todas las transformaciones previstas. Por ello es preciso emplear dos cajas. Evidentemente, en vez de la locomotora puede transformarse cualquier otra figura simple. Los niños inteligentes suelen llevar el juego hasta el limite de máxima dificultad, pidiendo que se cambien varios atributos al mismo tiempo. La figura 64 muestra una transformación difícil. Convertir la locomotora roja de la figura 64, que ya no puede identificarse como tal, en la locomotora amarilla de la figura 62 es una tarea muy atractiva. Si tenemos las dos figuras, pueden obtenerse las reglas de cambio de atributos a base de comparar los bloques que ocupan los mismos lugares correspondientes en dichas fi guras.
Juego 53
Adivinanza de figuras
El juego se inicia igual que los anteriores. Se construye una figura y se piden determinados cambios de atributos, simbolizados con cartulinas. Una vez realizada la transformación, se retira la figura que sirvió de punto de partida. Los niños de otra mesa deben descubrir la figura originaria con ayuda de las cartulinas indicadoras y de la figura transformada. La problemática resulta muy estimulante para niños inteligentes. Tomemos la figura roja y las cartulinas de la figura 64. La figura que se busca es la locomotora azul. En este juego sólo debe prestarse particular atención al cambio de color. La forma, el grosor y tamaño deben variarse según indican las cartulinas, que aparece invertido en la cartulina. La forma, el grosor y tamaño deben variarse según indican las cartulinas, ya que las flechas de doble sentido y la transformación inversa coincide en la dirección. Estas figuras curiosas y las cartulinas indicadoras que sirven de clave para resolver el acertijo dan lugar a gran variedad de ejercicios, que los niños realizarán con agrado.

















Comentarios
Publicar un comentario