MAESTRO ▅▅▅▅▅▅
PARALELO ▅▅▅▅▅
El término "maestro" deriva del sustantivo latino magister, que significaba: el que manda, dirige, conduce; de allí el director, el jefe, etc.; de allí el maestro que enseña, es decir, el que dirige o guía a los niños.
Vale la pena destacar algunos aspectos etimológicos de la palabra magister. Por su forma, se compone de dos partes, magis y ter. Esta última corresponde a un sufijo primitivo tero, que dio teros en griego y que significa "de entre dos", "uno de los dos", "aquél de dos que...". La parte magis se relaciona con magnus (grande) o, si se prefiere, con magis (más), o con maior (mayor que), términos todos que provienen de una raíz mag (que dio, en griego, megas y todos sus derivados); una forma, mago, tenía el sentido de "engrandecer", "honrar". De modo que "magister" significa, primariamente, el mayor o el más honrado entre dos; es decir, aquél a quien corresponde la dirección o el mando. Por ello "maestro" es no sólo el que enseña, sino el que educa, el que orienta, el que cultiva, el que muestra el camino, el que se pone al frente para que otros lo sigan, el que tiene autoridad para señalar a otros el rumbo y, por eso, el que es honrado y seguido, aceptado y mirado como el modelo cuyo ejemplo hay que seguir. ¡Terrible y grandiosa misión la del maestro!
A diferencia de magister, minister es el menor entre dos (de minus = menos, o de minor = menor), de donde provienen las significaciones de: servidor, doméstico, servidor (o ministro) de un culto, oficial subordinado, ministro, instrumento, agente, intermediario, sacerdote. El ministro está al servicio de algo o de alguien, es el subordinado de alguien, es el que está un escalón más abajo en una jerarquía cuyo superior lo tiene a su servicio.
Con el término "magister" se relacionan, además de "maestro", "magisterio", "magistral", "magistrado", etc. Con "minister" tienen que ver "ministerio", "ministerial", "administrar", "administrador", "administrativo", etc.
MATEMÁTICA ▅▅▅▅
El origen de este término es bastante curioso. Proviene del verbo griego manthano que significa, inicialmente, aprender, es decir, estudiar, instruirse, acostumbrarse, aprender de memoria; de allí, darse cuenta, remarcar, comprender. Del verbo deriva el sustantivo máthema, que denota el estudio, la ciencia, el conocimiento y, en particular, las ciencias matemáticas (que se denominaban, en la Grecia clásica: aritmética, geometría, astronomía y música, aunque en un sentido algo distinto del actual). El adjetivo mathematikós designa a quien se entrega al estudio y, en especial, a lo que se relaciona con la matemática. La ciencia matemática se caracterizaba con la expresión mathematiké téjne.
En realidad mathematiká eran las ciencias que el joven griego debía estudiar para formarse adecuadamente en la areté (término que podemos traduçir por "virtud", siempre que entendamos por ésta la perfección humana que se puede enseñar y de la cual la conducta moral es un aspecto; el hombre perfecto era, para los griegos, el sabio-bueno-bello). Las dos primeras disciplinas a las que se debía aplicar eran la ciencia de los números (aritmética) y la ciencia de las medidas (geometría). Luego seguían el estudio de las armonías (música) y de las esferas celestes (astronomía), a las que se solían agregar la geografía y la mecánica. Por tal razón la palabra "matemática" pasó a designar en especial las dos primeras de estas ciencias, que constituían, en cierta forma, el núcleo del saber.
Según cuenta Jámblico, autor neoplatónico del siglo IV , en su libro Sobre la vida pitagórica, los primeros en utilizar el término fueron los discípulos de esta escuela, que se dividían en mathematikói (o iniciados) y akustikói (u oyentes). Sin embargo, son los sofistas del siglo V a.C. quienes inician una verdadera sistematización de las disciplinas "matemáticas" con miras a la formación del ciudadano. La expresión probablemente más elaborada de esta intención pedagógica se encuentre en el diálogo Sobre la República de Platón que, en el libro VII y a partir de la alegoría de la caverna, desarrolla sus ideas acerca de las ciencias "matemáticas". De hecho, Platón insiste sobre estas disciplinas en muchos lugares de su obra, como el Menón, Las leyes, la Carta VII, y tantos otros, pero nos limitamos al libro VII de la República porque nos parece que presenta un buen resumen de sus ideas.
Los máthema de Pitágoras y sus seguidores, que eran simplemente los estudios, pasan a constituir, en Platón, un conocimiento científico riguroso, con un objeto único y una exigencia de fundamentación, metodología y sistema que se han de convertir en la base y el principio de lo que hoy llamamos "ciencia" y, sobre todo, de lo que denominamos "matemática".
Dice Alfred N. Whitehead:
MATEMÁTICA E HISTORIA DEL PENSAMIENTO
No iré tan lejos como para afirmar que construir una historia del pensamiento humano sin un profundo estudio de las ideas matemáticas de las sucesivas épocas es como omitir al personaje Hamlet en el drama que recibe su nombre de él. Eso sería pretender demasiado. Pero es, por cierto, análogo a excluir el papel de Ofelia. Este símil es singularmente exacto, pues Ofelia es completamente indispensable al drama, es muy encantadora —y un poco loca—. Admitamos, pues, que el estudio de las matemáticas es una locura divina del espíritu humano, un refugio ante la urgencia aguijoneante de los sucesos contingentes.
Dice Bertrand Russell:
MATEMÁTICA Y NATURALEZA
Nos vemos estimulados por nuestra experiencia a la creación del concepto del número; la relación del sistema decimal con nuestros diez dedos es suficiente para demostrar eso. Si uno puede imaginar seres inteligentes que vivan en el sol, donde todo es gaseoso, presumiblemente no tendrán concepto del número, ni de las "cosas". Podrían tener matemáticas, pero la rama más elemental sería la topología. Algún Einstein solar pudo inventar la aritmética e imaginar un mundo en el cual fuera aplicable, pero el tema sería considerado demasiado difícil para los escolares. Quizás, a la inversa, Heráclito no habría inventado su filosofía si hubiese vivido en un país del norte, donde los ríos se helasen en invierno. La influencia de la temperatura sobre la metafísica podría ser un tema amable para un nuevo Gulliver. Yo creo que la tendencia general de tales reflexiones es arrojar dudas sobre la teoría de que los conceptos surgen independientemente de la experiencia sensible.
MATEMÁTICA Y EDUCACIÓN
Aun a riesgo de provocar en algunas personas los sentimientos de horror y consternación que Paolo Ucello ha pintado tan maravillosamente en la Profanación de la Hostia, es necesario que manifestemos, porque la cuestión se plantea cada vez más y más, nuestro desacuerdo con las numerosas personalidades que, en la actualidad, piden a los científicos en general y a los matemáticos en particular que formen los miles de técnicos que necesitamos, según parece, para sobrevivir. Tal y como están las cosas, nos parece que en las "grandes" naciones superdesarrolladas científica y técnicamente en que vivimos, el primer deber de los matemáticos, y de muchas otras personas, sería proporcionar cosas que no les piden: hombres capaces de reflexionar por sí mismos, de despreciar los argumentos falsos y las frases ambiguas, y a los ojos de los cuales la difusión de la verdad importe muchísimo más que, por ejemplo, la Televisión planetaria en colores y en relieve: Hombres libres, y no tecnócratas- robot. Es tristemente evidente que la mejor manera de formar a estos hombres que nos faltan no es enseñarles ciencias matemáticas y físicas, que son ramas del saber en que lo normal es aparentar que se ignora hasta la existencia misma de los problemas humanos, y a las que nuestras altamente civilizadas sociedades conceden, lo que debería parecer paradójico, el primer lugar. Pero incluso al enseñar Matemática se puede, por lo menos, tratar de dar a las personas el gusto de la libertad y de la crítica, y habituarlas a verse tratadas como seres humanos dotados de la facultad de comprender.
R. Godement
(en prólogo) Curso de Álgebra,
Tecnos, Madrid, 1974.
MÉTODO ▅▅▅▅▅▅
Alrededor de "método" podemos encontrar todo un conjunto de palabras que tienen una relación más o menos estrecha con él: medio, instrumento, herramienta, así como analítico, sintético, etc.
▪ MEDIO, al igual que el término latino medium, del que proviene, es lo que está entre dos, lo que está en medio o en el medio, lo que relaciona dos términos o dos extremos. De allí que "medio" no se entienda sin relación con un término ("fin", del latín finis = remate, conclusión, límite, término) que le da sentido. No se puede entender "medio" sin aquello de lo que es medio. Por eso "medio" significa, también, aquello que se utiliza para llegar al término. Un medio que no lleve a un fin no tiene sentido.
▪ INSTRUMENTO proviene del latín instrumentum, compuesto, él mismo, por in (en este caso "hacia" o "para") y struo, verbo que significa "construir", "edificar". "Instrumento" es lo que sirve para construir, para armar, para producir, para realizar. Es el medio concreto que utilizamos para llegar al fin.
▪ HERRAMIENTA, del latín ferramentum y éste derivado de ferrum (hierro), designaba los instrumentos materiales, fabricados en hierro, que utilizaban los artesanos. Por extensión se aplica a todo instrumento de carácter manual, cualquiera fuere el material de que esté hecho.
▪ MÉTODO proviene del sustantivo griego méthodos, compuesto por metá (en medio de, entre) y odos (camino). "Método" es el camino que hay que seguir para llegar al fin, es el adecuado manejo de los medios para alcanzar el objetivo propuesto. El método implica tres cosas: 1) el conocimiento de los medios (la técnica); 2) la habilidad en su manejo (el hábito práctico); y 3) la planificación del uso de los medios para llegar del modo más rápido, seguro y fácil al fin propuesto.
El método supone siempre una manera reflexiva y ordenada de actuar, producto de una planificación consciente y eficaz. No hay métodos espontáneos o improvisados. La aparente espontaneidad de ciertas actuaciones metódicas es el producto de un largo aprendizaje y una intensa práctica.
Los métodos se pueden dividir según muy diversos criterios, pero veremos aquí sólo una división, señalada ya en la antigüedad griega y que se sigue utilizando en la actualidad.
▪ ANALÍTICO, derivado de "análisis", procede del griego análysis, compuesto de aná (de arriba hacia abajo, a través de) y lysis, que proviene, a su vez, del verbo lyo (soltar, desatar, cortar). El análisis es un proceso descendente, que resuelve el todo en sus partes, que desliga las partes unas de las otras para irlas tomando separadamente y, de este modo, verlas o estudiarlas de mejor manera.
▪ SINTÉTICO, del griego synthesis, formado por syn (con) y thesis (posición, tesis), es la composición, el unir o juntar lo que estaba separado, para integrarlo, o reintegrarlo, en una unidad. Es un proceso ascendente, de abajo hacia arriba, que reúne lo que estaba separado.
METRO ▅▅▅▅▅▅▅
Del griego metron, "medida", "instrumento para medir". Metro, sufijo, significa "lo que mide", "el aparato para medir".
Forma parte de numerosas palabras del lenguaje matemático o científico. (Parámetro, diámetro, geometría, goniómetro, barómetro, termómetro, calorímetro, anemómetro, etc.).
Dice Isaac Asimov (1):
Como todos, también yo busco el amparo y el apoyo de muchos mitos estimulantes. Uno de estos artículos de fe por el cual siento especial predilección consiste en afirmar que no se puede oponer ningún argumento en contra del sistema métrico decimal, y que las unidades que se usan comúnmente en los Estados Unidos constituyen un conjunto indefendible de tonterías que conservamos solamente por una especie de obstinación insensata.
Imagínese entonces la preocupación que me asaltó cuando hace poco me topé con una carta de un caballero inglés que denunciaba amargamente al sistema métrico como artificial, estéril y desconectado de las necesidades humanas. Por ejemplo, decía (y no lo cito textualmente), que si uno desea tomar cerveza, la medida adecuada es la pinta. Un litro de cerveza es demasiado y medio litro es demasiado poco, pero una pinta, eso sí es lo justo*.
* Antes de que me escriban para decirme que medio litro es más que una pinta, permítanme explicarles que si bien es cierto que es más que una pinta americana (0,473 litros), es menos que una pinta inglesa (0,569 litros). (N. del A.).
Por lo que yo puedo decirles, el provincialismo de este caballero era sincero, hasta el punto de llegar a creer que aquello a lo que uno está acostumbrado tiene la fuerza de una ley natural. Me recuerda a aquella inglesa devota que se oponía firmemente a la enseñanza de todo idioma extranjero levantando su Biblia y diciendo: "Si el idioma inglés le sirvió al profeta Isaías y a San Pablo Apóstol, también me ha de servir a mí".
Pero más que nada me recuerda que quiero escribir un ensayo acerca del sistema métrico decimal.
Para lograrlo, deseo comenzar diciéndoles que el valor del sistema no reside en el tamaño efectivo de las unidades básicas. Su valor consiste en que se trata de un sistema lógico. Las unidades están relacionadas entre sí de una manera razonable.
Todos los otros sistemas de medidas que yo conozco emplean un nombre distinto para cada unidad que representa una cantidad determinada. Para las distancias, los estadounidenses empleamos millas, pies, pulgadas, varas, estadios, cuadras, etc. Para los volúmenes, tenemos pecks, búshels, pintas, dracmas. Para los pesos tenemos onzas, libras, toneladas, granos. Nos pasa como a los esquimales, que se supone que tienen no sé cuántas docenas de palabras para decir nieve, pues emplean una palabra distinta cuando la nieve cae o cuando está quieta, cuando es blanda o cuando es dura, seca o húmeda, vieja o nueva, etcétera.
No dejamos de apreciar la ventaja de usar combinaciones de sustantivos y adjetivos. De esa manera empleamos el nombre como designación general para todas las clases de nieve y el adjetivo para describir cada variedad específica: nieve húmeda, nieve seca, nieve dura, nieve blanda, etc. ¿Cuál es la ventaja? Primero, que ahora apreciamos una generalización que antes no percibíamos. Segundo, que podemos usar los mismos adjetivos para otros sustantivos, y así tenemos roca dura, pan duro, corazón duro y, en consecuencia, disponemos de una nueva generalización: la dureza.
Que yo sepa, el sistema métrico decimal es el único sistema de medida que ha alcanzado esta etapa de desarrollo.
Comencemos con una medida arbitraria de longitud, el metro (del latín metrum o del griego metron, que significan "medir"). Tomando esa palabra como la denominación genérica de longitud todas las unidades de longitud serán metros. Para diferenciar una unidad de longitud de otra usemos un adjetivo. En mi opinión ésa es la forma de arreglar las cosas.
A decir verdad, los adjetivos que se emplean en el sistema métrico (supongo que para que no se lleguen a perder por accidente) están sólidamente unidos a la palabra genérica de manera que se convierten en prefijos. (Por cierto, amable lector, que al hacer esto con el sistema de medidas han dejado "todo prefijado".).
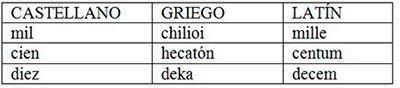
Los prefijos fueron tomados del griego y del latín de acuerdo con la siguiente tabla:
Ahora bien, si reservamos los prefijos griegos para las unidades grandes y los latinos para las pequeñas, tenemos:
No interesa cómo es de largo un metro; todas las demás unidades de longitud ya están definidas. Basta con que usted conozca la longitud del metro, ya sea en yardas o en longitudes de onda de la luz o mediante dos marcas en una vara, para que automáticamente sepa cuáles son las longitudes de todas las otras unidades. Además, al hacer que todos los submúltiplos varíen según potencias de diez, se hace muy fácil convertir una unidad en otra (debido a que nuestro sistema de numeración es decimal). Por ejemplo, yo puedo decirles de inmediato que en un kilómetro hay exactamente un millón de milímetros. A ver si usted me dice ya mismo cuántas pulgadas hay en una milla.
Y además, una vez que usted ha memorizado los prefijos, le servirán para cualquier tipo de medición. Si le dice que un "poise" es una unidad de viscosidad, no importa cuán grande es dicha unidad ni de qué manera está relacionada con otros tipos de unidades y ni siquiera interesa saber con exactitud qué es la viscosidad. A pesar de no saber absolutamente nada de un tema uno sabe que un centipoise equivale a un centésimo de un poise, que una hectárea es igual a cien áreas, que un decibel es un décimo de bel; e incluso que un "kilodólar" equivale a mil dólares*.
* Si alguien me quiere escribir para decirme que un militar es un milésimo de tar y que un centitar equivale a diez militares, pueden hacerlo... pero no les voy a hacer caso. (N. del A.).
MULTIPLICAR ▅▅▅▅
Proviene del verbo latino multiplico, que significa "aumentar", "acrecentar". Está compuesto por multus (mucho) y plico (plegar, replegar, enrollar). El significado primario de multiplico es el de "plegar mucho", de donde "aumentar mucho", que conduce directamente a multiplicar.
El verbo latino plico está emparentado con el verbo pleko, que significa "trenzar" o "unir". Con ellos también se emparenta el latín plecto, "entrelazar". A esta familia pertenecen los compuestos a-plico, com-plico, ex-plico, im-plico, su-plico.
La palabra "multiplicar" quiere decir "mucho-plegar", así como triplicar, cuadriplicar, etc. significan tres-plegar, cuatro-plegar, etc. Esto nos advierte que la multiplicación ha significado -y tratándose de números naturales es obvio- una suma abreviada: 3 x 2 da el mismo pos de dos que 3 veces 2. Esta idea predomina desde la antiguedad; claro que hay ejemplos de discrepancia aparente. Así, en una aritmética inglesa de 1677 leemos estas palabras:
"La multiplicación se efectúa entre dos números de análoga clase para producir un tercer número tal que se hallará en la misma razón con el primero, que el segundo con la unidad".
a . b = c significa c/a = b/1
En su obra "Institutione Arithmeticae", Severino Boecio (480-524) utiliza los términos ducere, producere, facere, como sinónimos de multiplicar. Las voces producto y factor desciende de aquel libro.
El signo x, en forma de cruz de San Andrés, tuvo origen en cierto procedimiento de multiplicar en cruz.
El signo . , fue introducido por el inglés Thomas Harriot (1560-1621) cuando había que señalar producto entre números y letras o entre letras solas (para evitar la confusión con x).
Luca Pacioli (1445-1514?) recoge las enseñanzas del "Lilavati" de Bhascara (1150) y explica ocho procedimientos para multiplicar. A uno de ellos lo llama "Bericocoli vel Scahchierij" que traducimos por "tablero". Es el método nuestro, impracticable en el ábaco:
Del latín norma, "escuadra para arreglar y ajustar las piedras, las maderas y otras cosas". En sentido figurado "regla" o "ley".
De ella deriva normalis, "perpendicular", "hecho a escuadra", "hecho con la escuadra".
ORIGEN ▅▅▅▅▅▅▅
Deriva del sustantivo latino origo ( proveniencia, nacimiento, causa , fuente, principio) que, a su vez, proviene del verbo orior, "levantarse", en los sentidos de "salir de la cama", "ascender los astros", "brotar las plantas", "nacer", "originarse", "tener su comienzo". De modo que, origen es el lugar en el que nace o comienza algo. Su aplicación matemática es inmediata.
Cf.: oriente, originalidad, oriundo.
Compuesto de los términos griegos para, "junto a" y al-lélon, que significa "el uno al otro" (al-los, "otro"). De modo que paralelo significa "uno junto al otro" o "uno al lado del otro".
PERPENDICULAR ▅▅
Del latín perpendiculum, "plomada", derivado de perpendo, que significa "pesar cuidadosamente".
El verbo pendo, significa "dejar pender los platillos de una balanza"; de allí, "pesar" y, figuradamente, "apreciar". En sentido intransitivo significa "estar pesando".
El intensivo del verbo pendo, que es penso, "pesar", etc., además de los sentidos materiales de "pesar" tiene el sentido de "sopesar", "tomar el peso", "calcular el valor". De allí, "pensar", "pensamiento", etc.
causa, fuente, principio) sentidos de "salir de la "originarse", "tener su comienza algo.
POLÍGONO ▅▅▅▅▅
POLIEDRO ▅▅▅▅▅▅
Viene de polyedros, compuesto de polys (mucho-s) y hedra, "asiento", "base". De manera que poliedro significa "de muchas bases".
Del significado de "puesto" -de allí "residencia"- que tiene el término hedra, provienen cátedra, catedral e, inclusive, cadera, que significaba, originariamente, "el respaldo de la silla".
Cf.: diedro, triedro, tetraedro, hexaedro, dodecaedro, icosaedro.
PROBLEMA ▅▅▅▅▅
El término "problema" deriva directamente del griego próblema, compuesto de pro (delante) y blema (lo que se arroja o tiende), que proviene, a su vez, del verbo bállein (echar, arrojar). Es decir, "problema" significa lo que ha sido arrojado delante, el obstáculo, la piedra que nos obstruye el camino.
El problema es una situación frente a la cual no podemos menos que adoptar una actitud. Esta actitud puede consistir en una de las tres siguientes opciones:
1. Dar marcha atrás y desandar el camino. En este caso retrocedemos ante el obstáculo y renunciamos a proseguir nuestro itinerario.
2. Buscar alguna forma de rodearlo, cambiando de rumbo o eligiendo alguna ruta alternativa, u otra forma de locomoción. Es decir, esquivamos el problema en lugar de encararlo.
3. Enfrentar el obstáculo y buscar la forma de removerlo del camino, o de dejar la ruta despejada para poder proseguir. O sea, encaramos el problema.
Encarar el problema significa enfrentarse a él, analizarlo y buscar la manera de eliminarlo. Esta actitud intelectual se resume en la pregunta que nos conduce a una respuesta, a través de la cual esperamos encontrar la solución.
Pregunta es un sustantivo derivado del verbo "preguntar" que, a su vez, proviene del latín percuncto, formado por per (a través de) y cunctus (todo), es decir, "explorarlo todo", "inquirir", "indagar", "investigar". La pregunta es una forma de investigar la cosa. No consiste sólo en interrogar, pues algunas interrogaciones no son preguntas en sentido propio; por eso se las llama "preguntas retóricas", "preguntas formales", "falsas preguntas". El adjetivo con el que las acompañamos señala el sentido equívoco que tiene aquí el término "pregunta". Para que una interrogación sea verdaderamente pregunta, debe cumplir con cuatro condiciones: 1) que quien pregunta no sepa de antemano la respuesta; 2) que quien pregunta sepa qué cosa ignora; 3) que la pregunta tenga una respuesta posible (no inmediata, sino posible); 4) que la respuesta tenga algún interés para el que pregunta.
Toda pregunta establece un campo y una dirección en la investigación del problema. Recordemos que la pregunta no es una situación, sino una actitud frente a una situación. La pregunta determina el carácter de la respuesta (si se pregunta "cuándo", la respuesta será un tiempo; si "cómo", la respuesta indicará un modo; si "cuánto", una cantidad; etc.). Pregunta y respuesta son estrictamente correlativas.
Respuesta es un antiguo participio del verbo "responder" que, a su turno, proviene del latín respondeo, formado por re (otra vez, de nuevo) y spondeo (prometer), es decir, "prometer a su turno", "pagar a su vez", de donde "comprometerse a", "corresponder a" y "responder a".
Como la respuesta es rigurosamente correlativa de la pregunta, a saber, con la actitud de la que se parte, puede o no coincidir con la solución, o sea, con la situación de eliminar el problema.
Solución proviene del latín solutio, derivado a su vez del verbo solvo, que
significa "soltar", "desatar", "deshacer", "librar", "desenvolver", "desechar".
"Solución" es el acto de desatar, deshacer, desenredar, o desembarazar. Es la situación de eliminar el problema.
PUNTO ▅▅▅▅▅▅▅
Del latín punctum, que significa "picadura". De allí "la marca" o "el pequeño agujero hecho por la picadura". De allí "el agujero en un conducto de agua", "el pico" o "todo pequeño agujero" y, de allí, "punto".
Viene del verbo pungo, "picar" o "perforar".
Los pitagóricos decían que el punto es una monada con posición. La monada es lo indivisible. Platón afirmó que el punto era una ficción geométrica y que no era sino el comienzo de la línea. Aristóteles explica que, además, el punto no es un cuerpo y carece de peso; no es posible distinguir un punto (stigmé, "la marca") del lugar (topos) por él ocupado.
Euclides, Arquímedes y otros prefirieron la voz semeíon (marca, signo) y así la definición 1 de Los Elementos (Euclides) dice: Semeíon es aquello que no tiene partes.
Para los contemporáneos, punto es un concepto primitivo. (Del mismo modo que recta, plano y espacio).
LÍNEA
Del latín linea, "línea", de lineus, "hilo de lino".
_____________________
Referencia Bibliográfica
(1) ASIMOV, I.- De los números y su historia. Buenos Aires, Librería "El Ateneo" Editorial, 1981.















.jpg)







Comentarios
Publicar un comentario