Reconocimiento es el principio del agradecimiento o estimación que hacemos del beneficio recibido.
La acción de alabar implica el manifestar con palabras la satisfacción o admiración que nos produce alguien o algo.
En nuestro caso, es para referirnos al Maestro Jean-Jacques Parot y a su excelente trabajo titulado Actualización Matemática. Didáctica de la Matemática en los primeros niveles, que tiene como marco editorial la permanente calidad de la Editorial TEIDE.
Su convocatoria, de pura estirpe dienesiana, es menester para todos aquellos que son maestros de buen grado.
Reverso de la portada
Prólogo
« Proponemos que la educación permanente sea la piedra angular de la política educativa en los próximos años, tanto en los países desarrollados como en los países en vías de desarrollo»1. En función de estos objetivos, es al educador a quien concierne ante todo considerar y renovar continuamente sus conocimientos y su actitud frente a sus alumnos a fin de adecuar sus enseñanzas a unos objetivos en constante evolución2.
La finalidad de esta obra es proporcionar una ayuda al educador, que le permita dar los primeros pasos —tal vez los más difíciles— hacia una formación continua en matemática. El libro contiene los conocimientos básicos indispensables para la enseñanza de la matemática moderna en los primeros niveles. Nuestra intención es que a través de estos conocimientos el profesor saque el máximo partido de las guías específicas para cada curso y para cada tema, y que los padres puedan entender el camino que siguen sus hijos en sus estudios.
En la exposición, se han seguido básicamente las teorías del profesor Zoltan P. Dienes sobre el aprendizaje en matemática3, teorías que si en un principio pudieron parecer arriesgadas, ahora, tras largos años de experimentación en escuelas de los cinco continentes, han demostrado su validez y madurez. Presentamos siempre situaciones muy sencillas y a partir de las mismas se destacan los conceptos matemáticos. Tal vez algún matemático «profesional» encontrará trivial el contenido, sin embargo nuestra experiencia nos lleva a la conclusión de que la causa de muchos fracasos en los cursos de actualización es precisamente el desdeñar esta primera etapa. Es más, sugerimos que en los cursos de actualización de los profesores se trabajen los materiales y se expongan los contenidos en la misma forma que los profesores trabajarán con sus alumnos. Hay que conseguir que el curso no se convierta en una serie de conferencias «ex catedra», en unos consejos teóricos —difíciles de aplicar en la práctica— para conseguir un cambio de actitud en los educadores. Recordemos una vez más que en la enseñanza de la nueva matemática el profundo cambio introducido no aparece sólo en los contenidos sino también en la metodología para llegar a ellos.
El material más utilizado a lo largo de esta obra son los Bloques Lógicos. Este material existe fabricado en plástico de colores opacos, en plástico transparente para ser proyectado, en madera pintada de distintos tamaños, pero para mayor facilidad del lector, en las últimas páginas de esta obra, hemos incluido unas hojas de colores que permiten fabricar fácilmente un material válido, simplemente recortándolas o bien copiándolas sobre cartulina de colores. Recomendamos utilizar además otros materiales complementarios; la diversidad de materiales nos conducirá insensiblemente a la abstracción4.
Uno de los materiales más adecuados para la comprensión de la numeración en las distintas bases (capítulo 3) son, sin duda, los Bloques Multibase de Dienes. Es un material fabricado sencillamente, en madera pulida sin color alguno, a fin de conseguir una mayor abstracción5.
Esta obra será, sin duda, también útil para quienes, por el motivo que sea, no pueden asistir a cursos de actualización conducidos por un profesor. En este caso recomendamos especialmente conseguir formar un pequeño equipo de trabajo para estudiar y trabajar el texto en colaboración. Se conseguirá así adquirir el dinamismo que es fundamental en la adquisición de los conceptos.
Esperamos que este libro contribuya a proporcionar al lector el deseo y la posibilidad de utilizar textos de niveles más avanzados6 y, concretamente al profesor, un instrumento eficaz para la preparación de sus clases.
_______________________
1. 21 puntos para una nueva estrategia de la educación. — « El Correo de la Unesco» (Paris), XXV, noviembre (1972). Una ampliación y un comentario a este ambicioso programa los hallará el lector en la obra de P. Lengrand, Introducción a la educación permanente, publicada en coedición por Editorial Teide y Unesco (Barcelona 1973).
2. Edgar Faure: Apprendre a être. —Unesco-Fayard. —Paris.
3. Z. P. Dienes: Las seis etapas del aprendizaje en matemática. —Editorial Teide (Colección Enseñanza de la Matemática Moderna, VII). —Barcelona 1971.
4. Recomendamos, por ejemplo, como materiales lógicos estructurados, el Trimat y el Cuadrimat. Existen fabricados en plásticos de colores, pero se suministran también en cartulina troquelada en el cuaderno de trabajo Trimat/Cuadrimat de Dienes-Mézard, publicado por Editorial Teide (Barcelona 1972).
5. Consúltese el folleto Cómo utilizar los Bloques Multibase de Dienes, con numerosos ejercicios.
6. En la bibliografía que aparece en las últimas páginas de esta obra se citan algunas obras fundamentales. En ellas, además, el lector interesado encontrará una amplia bibliografía complementaria.
ADLER, I.: The New Mathematics. —Dobson. —London 1959 (en rústica, Mentor Books. —1960).
ADLER, 1.: Thinking Machines. — Dobson.— London 1961.
BRÉARD, C.: Mathématiques 5e —2e. —Éditions de l'Ecole. —Paris 1961.
COLOMB, J.; GAGNAIRE, P.; GLAYMANN, M.; SARGENT, J.: Fichas perforadas, a través de los conjuntos, la lógica y la numeración.—Versión y adaptación D. BERGADÁ. —Teide. —Barcelona 1973.
Cómo utilizar los Bloques Multibase de Z.P. Dienes. —Teide. —Barcelona 1971.
DIENES, Z.P.: La matemática moderna en la enseñanza primaria. —Teide. —Barcelona4 1972.
DIENES, Z.P.: Estados y operadores (I vol.: Operadores aditivos; II vol.: Iniciación al álgebra; III vol.: Operadores multiplicativos). —Teide. —Barcelona 4 1971, 1971, 1972.
DIENES, Z.P.: Las seis etapas del aprendizaje en matemática. —Teide. —Barcelona 1971.
DIENES, Z.P.: Fracciones. —Teide. —Barcelona 1972.
DIENES, Z.P.; GOLDING, E.W.: La geometría a través de las transformaciones (I vol.: Topología. Geometría proyectiva y afín; II vol.: Geometría euclidiana; III vol.: Grupos y coordenadas). —Teide. —Barcelona2 1972, 1969, 1970.
DIENES, Z.P.; GOLDING, E.W.: Los primeros pasos en matemática (I vol.: Lógica y juegos lógicos; II vol.: Conjuntos, números y potencias; III vol.: Exploración del espacio y práctica de la medida). — Teide. — Barcelona 61972, 41972, 41973.
FÉLIX, L.: Exposé moderne des mathématiques élémentaires. — Dunod. —Paris 1959.
FLETCHER, T.J.: Didáctica de la matemática moderna en la enseñanza media. —Teide. —Barcelona 21971.
GLAYMANN, M.; ROSENBLOOM, P.C.: La lógica en la escuela. —Teide, 1974. —Barcelona.
KOTHE, S.: Cómo utilizar los Bloques Lógicos de Z.P. Dienes. —Teide,1974. —Barcelona.
PAPY, G.: Groupes. Presses Universitaires. —Bruxelles 1961.
PIAGET, J.; INHELDER, B.: La genèse des structures logiques élémentaires. —Delachaux & Niestlé. —Neuchâtel-Paris.
PIAGET, J.; y otros: L'enseignement des mathématiques. —Delachaux & Niestlé. —Neuchâtel-Paris.1955.
REVUZ, A.: Mathématique moderne, mathématique vivante. — O.C.D.L. Paris. (Versión y adaptación castellana por Luis M. Santaló: Matemática moderna, matemática viva. —Elementos. —Buenos Aires 1965.)
SERVAIS, W.; VARGA, T.: Teaching School Mathematics. —Penguin Books - Unesco. —1971.
VARGA, T.: Ordinogramas, fichas perforadas y probabilidades. Juegos matemáticos. — Teide, 1974. —Barcelona.
ZIGLON, R.; Vers les structures. —Hermann. —Paris 1971. (Versión castellana de Rosa Foix, en preparación: En busca de las estructuras. Nueva pedagogía de la matemática. —Teide. —Barcelona.)
4 Algo de lógica matemática
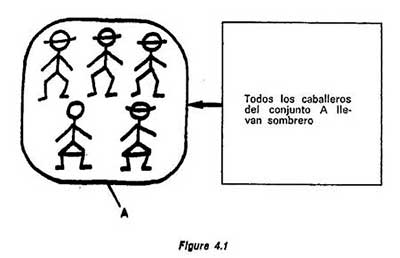
Construyamos dos conjuntos A y B, consideremos sobre cada uno de ellos la proposición:
«Todos los caballeros del conjunto llevan sombrero» (figura 4.1).
Estaremos de acuerdo al decir que esa proposición es verdadera, puesto que no podemos indicar uno que no lleve sombrero.
Ahora, si decimos: «Todos los caballeros del conjunto B llevan sombrero » (figura 4.2), comprobamos que esta proposición es falsa porque podemos señalar uno que no lleva sombrero.
Pero si no se puede encontrar por lo menos uno que no cumpla la condición, entonces no se puede decir que la proposición sea falsa; así por ejemplo en el conjunto C (figura 4.3) tenemos que si decimos: «Todas las niñas del conjunto C llevan sombrero» (figura 4.3), no se puede afirmar que la proposición sea falsa porque no existe en C una niña que no lleve sombrero.
Consideremos ahora una proposición cualquiera, y distingámosla de su negación y de su proposición contraria (figura 4.4).
Representemos por el símbolo p la proposición «En cada taza hay café» y designemos como «no p » la negación de p y como «co p» lo contrario de p. Veamos si estas proposiciones son ciertas o falsas, colocando el resultado en un cuadro (figura 4.5).
Conclusión. Para que la negación de una proposición sea cierta (o que la proposición sea falsa) es suficiente que haya un elemento el cual no la cumpla. Para que la contraria de una proposición sea verdadera es necesario y suficiente que todos los elementos no la cumplan.
Imaginemos la situación de la figura 4.6.
«Todos los caballeros del conjunto D llevan sombrero.»
Luego:
Podemos afirmar que esa proposición es cierta en el conjunto anterior pero no lo es en cualquier conjunto. En el conjunto E (figura 4.7) existe un caballero que no lleva sombrero («existe un» se debe entender como «existe por lo menos un» lo que a veces se representa por el símbolo ∃); entonces, en ese caso:
Figura 4.7
Consideramos ahora el referencial F (figura 4.8).
El conjunto de las personas que llevan sombrero es un subconjunto del conjunto de los caballeros (por no tener sino un elemento este conjunto se llama conjunto unitario).
________________________________
Podemos afirmar
Pero se puede también decir que el conjunto de los caballeros no es subconjunto del conjunto de las personas que llevan sombrero y
Aparece entonces una relación entre la noción de subconjunto y la noción de implicación.
De una manera general, sea el conjunto F; designemos como F (p) el subconjunto de los elementos de F que tienen la propiedad p; de la misma manera, designemos como F (q) el subconjunto de los elementos que tienen la propiedad q.
Por ejemplo: p = ser dama
q = no llevar sombrero
Para estas condiciones, en la figura 4.8 tenemos que F (p) es el subconjunto llamado D de las damas del conjunto F y F (q) es el subconjunto de los elementos de F que no llevan sombrero, designado por la letra S.
No debemos considerar lo que acabamos de decir como una definición de la implicación, pues existen implicaciones de otro tipo. Por ejemplo: si llueve entonces llevo mi paraguas.
Desde luego si en un estacionamiento el conjunto de los autos blancos es un subconjunto de los autos americanos, entonces podremos decir que, en el conjunto de autos de dicho estacionamiento,
Consideremos la propiedad q: «no llevar sombrero»; en la figura 4.9, G (q) es un subconjunto de G: G (q) tiene tres elementos.
Consideramos la propiedad r: «ser caballero»; en la figura 4.9, G (r) es un subconjunto de G; G (r) tiene dos elementos.
A una propiedad siempre le corresponde un subconjunto.
Consideremos la propiedad s: «ser animal»; en la figura 4.9 diremos también que G (s), o sea, el conjunto de los elementos de G que tiene la propiedad de ser animales es un subconjunto de G; ocurre en este caso que G (s) no tiene ningún elemento, es el conjunto vacío que representamos por ∅ .
Procediendo de esta manera se podrá siempre considerar el conjunto vacío como subconjunto de cualquier conjunto.
Ejemplo. Sea el conjunto P de los enteros pares. El conjunto vacío es un subconjunto de P (lo que escribiremos ∅ ⊂ P). En efecto, el conjunto de los elementos de P que no son múltiplos de dos es un subconjunto de P pero, como resulta que todos los números pares son múltiplos de dos, entonces el conjunto de los elementos de P que no son múltiplos de dos es el conjunto vacío. Conclusión: ∅ ⊂ P.
Sea H (figura 4.10) un conjunto de figuras. H es nuestro referencial. En este conjunto las figuras están pintadas de un solo color.
Sea H (d) el subconjunto de los círculos de H. Es evidente que H (d) es un conjunto vacío:
H (d) = ∅
Pero, según lo dicho anteriormente, como H (d) es el conjunto vacío, H (d) se puede considerar también como subconjunto de H (a), subconjunto de los elementos de H que son azules.
(Es cierto que no se puede encontrar en el conjunto H un circulo que no sea azul).
Por otra parte, si se designa por H (n) el subconjunto de los elementos de H que son negros , se puede decir también que el subconjunto H (d) de los discos* de H es un subconjunto de H (n) pues, según lo visto anteriormente, H (d) es vacío y el conjunto vacío es un subconjunto de cualquier conjunto.
(Es cierto que no se puede encontrar en el conjunto H un círculo que no sea negro).
Pero si consideramos las dos implicaciones:
pues si un elemento es negro no es azul.
Llegamos entonces a la situación en que un elemento a la vez tiene una propiedad y no la tiene; esto no puede ser sino en el caso de que el conjunto de tales elementos sea el conjunto vacío.
Si un conjunto E no es vacío y consideramos cierta propiedad p, admitiremos en matemática que no hay sino dos posibilidades para cualquier elemento de E:
– o este elemento cumple con p.
– o este elemento no cumple con p.
Para probar que un conjunto es vacío se podría entonces probar que sus elementos cumplen a la vez con una propiedad y con la negación de la misma.
Ejercicio n.º 1. Consideremos la proposición p, siguiente: «Todos los elefantes del polo Sur son verdes».
¿Es cierto o falso?
Es cierto porque en el polo Sur no se puede encontrar ningún elefante no verde.
Ejercicio n.º 2. Consideremos la proposición p₂: «Todos los elefantes del polo Sur son no verdes».
¿Es cierto o falso?
Es cierto porque en el polo Sur no se puede encontrar ningún elefante verde.
Ejercicio n.º3. Si a una persona que no sabe nada del polo Sur pero sabe lógica matemática se le dice: «Las proposiciones p₁ y p₂ son ciertas, ¿qué puede concluir este extranjero?
El conjunto de elefantes es tal que sus elementos cumplen a la vez con una propiedad y su negación; entonces ese conjunto es vacío, de tal manera que se puede concluir: en el polo Sur no vive ningún elefante.
Ejercicio n.º 4. Consideremos las situaciones de la figura 4.11.
Analicemos en cuáles conjuntos las siguientes proposiciones, son ciertas.
* disco: término equivalente a "circulo"
RECOMENDACIÓN
Recomendación quiere decir aviso o encargo dejado a alguien para que lo tenga presente, no se olvide y pueda ocuparse de lo mismo.
Ambos textos están a vuestra disposición en nuestra página pudiendo acceder a ellos a través de los enlaces que figuran en los respectivos títulos.






























.jpg)


Comentarios
Publicar un comentario