
Podemos establecer transformaciones funcionales a partir, por ejemplo, de condiciones de cambio de color. Formamos dos equipos de niños cada uno de los cuales posea un juego completo de bloques.
►Un primer juego puede consistir en hacer que los niños de uno de los equipos construyan una figura cualquiera en disposición de mosaico. Los niños del otro equipo tendrán que reproducirla exactamente con sus piezas. A continuación es el segundo equipo quien realiza la construcción y el primero el que la copia.
►En un segundo juego, la reproducción de la figura original debe hacerse sabiendo que, por ejemplo, las piezas rojas se transforman en amarillas y recíprocamente, las amarillas en rojas; las piezas azules permanecen azules. Los restantes atributos de las piezas permanecen invariantes. Dada la figura inicial, siempre puede construirse su reproducción reemplazando las piezas de cada color por aquellas del color en el cual deben transformarse según las reglas dadas.
Son muchas las transformaciones posibles en cuanto a color. Por ejemplo, el rojo se puede transformar en azul; el azul en rojo y el amarillo permanecer amarillo.También podría establecerse que: el rojo cambia en amarillo, el amarillo en azul y el azul en rojo.
Así los niños tienen muchas posibilidades para la invención de diferentes funciones. Es decir, el niño no sólo construye las figuras imágenes a partir de reglas dadas por otros, sino que establece reglas propias para la transformación. Por supuesto es posible trabajar con funciones que transforman las formas o bien el número de puntos. Del mismo modo pueden combinarse estas transformaciones simultáneamente. Los grados de complejidad dependerán de los grados de capacidad de los niños que participen del juego.
Puede resultar interesante, proponer a los niños juegos del siguiente tipo:
I.- Esta máquina cambia el color.
Coloca otras piezas en la entrada y dibuja las piezas que encontrarás en la salida.
II.- Estas máquinas cambian la forma; coloca en las entradas piezas de tu elección y dibuja las piezas que se hallarán en las respectivas salidas.
III.- Aquí tenemos más máquinas.¿Qué pieza se halla en la salida de la máquina A?
¿Qué pieza se halla en la salida de la máquina B?
¿Qué observas?
La máquina A y la máquina B son máquinas equivalentes .
Dos máquinas son equivalentes, si para la misma pieza colocada en la entrada se obtiene, para las dos máquinas, la misma pieza en la salida.
Coloca piezas de tu elección en la entrada de estas máquinas y dibuja las piezas que se hallarán en las respectivas salidas, de acuerdo con las reglas establecidas.
►Jugando en una tabla.
A partir de condiciones de cambios de forma, uno de los niños ha propuesto las siguientes reglas para el cambio:
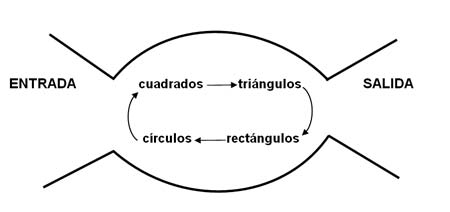
"Todo bloque triángulo se transforma en cuadrado; todo bloque cuadrado se transforma en rectángulo; todo bloque rectángulo se transforma en círculo y todo bloque círculo se transforma en triángulo. No cambian ni el color, ni el tamaño, ni el número de puntos."
Esquemáticamente:
Otros niños han construido, dibujándola en el piso, una tabla con dos columnas.
El primer jugador coloca en el primer casillero de la columna objeto una pieza a su elección, describiéndola por sus atributos. Otro niño, previo enunciado de las reglas de cambio, colocará en el casillero vecino de la columna imagen, la pieza correspondiente. Luego de completarse los casilleros siguientes según el mismo procedimiento, suele ocurrírsele a algún niño colocar la pieza elegida en casillero de la columna imagen.
La nueva situación significa conocer la pieza imagen y descubrir, habiéndose mantenido las reglas de cambio establecidas, cuál es la pieza objeto para esa imagen.
En el caso presentado, la pieza objeto es (cuadrado, rojo, grande, con punto).
Más adelante podemos presentar la siguiente situación:
Hemos colocado el objeto y la imagen . Los niños deben decidir si la pieza imagen es la que corresponde, según las reglas establecidas, para la figura objeto. Si esta imagen no es la correspondiente, deberán justificar el porqué y acto seguido, retirar la "falsa imagen" y reemplazarla por la que verifica las reglas.
También es importante proponer juegos para lograr el descubrimiento de reglas. En este caso, presentamos varios pares de bloques objeto-imagen. Por ejemplo:
Los niños, de acuerdo con las correspondencias dadas, deberán descubrir las reglas de cambio. En el ejemplo indicado deben obtenerse:
►Otro juego
Podemos imaginar una máquina que cambia la forma: cada vez que haga su entrada un bloque lógico será transformado en otro bloque lógico de acuerdo con las siguientes reglas de cambio:
color no cambia; número de puntos no cambia; tamaño no cambia.
Para comenzar las máquinas no serán representadas sobre papel o cartón sino concretizadas por los mismos niños. Se formarán equipos de cinco niños uno encargado de la "entrada", otro de la "salida"; un tercero de la "máquina", el que estará asociado a un "suministrador". El quinto niño será el encargado del "tablero de recepción".
El niño "entrada" recibe, al comenzar el juego, una bolsita con un número determinado de bloques, no conociendo el detalle del contenido Saca una de ellas y , luego de analizarla, la describe por sus atributos: "rojo, cuadrado, grande, un punto". Recibida esta información, el operador de la "máquina" enuncia los cambios que ella produce: "no cambia color; no cambia número de puntos, no cambia tamaño, cambia cuadrado en triángulo. El "suministrador", que tiene en su poder un juego de bloques lógicos completo, selecciona el transformado correspondiente y lo entrega al "operador" de la máquina. Éste, a su vez, lo entrega al niño "salida" quien lo describe: "rojo, triángulo, grande, un punto". Finalizado el proceso de cambio, el niño encargado del tablero de recepción retira la pareja "bloque de entrada- bloque de salida" y los ubica en un tablero a dos columnas: objeto-imagen. Una vez terminada la transformación de las piezas de entrada, el encargado del tablero verifica que se hayan cumplido las reglas de cambio.
La versión del juego en el aula es, por supuesto, creación del maestro, quien lo enriquecerá en el plano del entretenimiento y la competición. Convendrá repetir frecuentemente este juego, con distintas clases de "máquinas" y permutando los papeles que representan los niños. Además, pueden "empalmarse máquinas entre sí. Es decir, la salida de la primera máquina puede ser considerada como entrada de la segunda máquina que, finalmente, dará el resultado producido por "la máquina compuesta".
Más juegos:
► Operador forma y operador color.
Referencial: los bloques lógicos grandes sin punto.
Trabajaremos en este juego con los siguientes operadores:
Por la función "negra" el triángulo rojo se transforma en el círculo rojo. Aplicando la función "rayada" al triangulo rojo se obtiene el triángulo amarillo. Si se aplican al mismo tiempo la función "negra" y la función rayada" al triángulo rojo se obtiene el círculo amarillo. Si aplicamos las dos funciones al círculo amarillo obtenemos el rectángulo azul, etc. ¿Cuántas veces debe aplicarse cada una de las funciones al rectángulo rojo para volver al rectángulo rojo?
(Continuar la tabla hasta llegar, para cada operador, nuevamente al rectángulo rojo)
Una ampliación interesante puede ser la de asociar la composición de las funciones "negra" y "rayada" de este juego al movimiento de la aguja de las horas en un reloj.
Si el rectángulo rojo se asocia al 9 del reloj, completar el siguiente esquema:
► Cambiemos el trencito por ?
Referencial: todos los bloques lógicos.
Dado el trencito
aplicarle los operadores siguientes:
► Casitas y bloques
Con los bloques lógicos armar seis casas y ubicarlas como indica el siguiente dibujo:
Para este juego consideramos los atributos forma, color y tamaño, sin tener en cuenta que cada pieza en cuestión tenga o no tenga punto.
a) ¿Qué es lo que no cambia en las casitas cuando se traspone la línea azul?
b) ¿Qué es lo que no cambia en las casitas cuando se traspone la línea roja?
c) ¿Qué es lo que no cambia en las casitas cuando se traspone la línea amarilla?
d) ¿Qué es lo que cambia en cada uno de los tres casos precedentes?
►Siempre con casitas y bloques
Sobre la base del esquema del juego anterior, ahora haremos un juego que consiste en "saltar por encima de una casa", como lo indica el dibujo siguiente:
a) ¿Qué se produce en las casas ordenadas según el dibujo del juego anterior cuando se salta sobre una casa?
- Lo que estaba azul se transforma en ......................................
- Lo que estaba rojo se transforma en ......................................
- Lo que estaba amarillo se transforma en ......................................
b) Efectuar un nuevo ordenamiento de las casitas de modo que:
- el calor del techo no cambie cuando se atraviese la línea azul;
- el color de la ventana no cambie cuando se atraviesa la línea roja;
- el color de la pared no cambie cuando se atraviesa la línea amarilla;
En este nuevo ordenamiento, ¿qué ocurre si se salta por encima de una casa?
- el color de la ventana se convierte en el color de ......................................
- el color del techo se convierte en el color de ......................................
- el color de la pared se convierte en el color de ......................................
- ¿cuál es el operador inverso de cada uno de los operadores?
- ¿qué ocurre si se componen un operador y su inverso?
Bibliografía:
Dienes, Z. (1977). Juegos con materiales estructurados en la actividad matemática. Tomo I: Trimat.Cuadrimat. Buenos Aires: Gram Editora.
Dienes, Z. (1977). Juegos con materiales estructurados en la actividad matemática. Tomo II: Bloques lógicos. Buenos Aires: Gram Editora.























Felicitaciones para sus alumnos.
ResponderEliminarY en especial para los tres docentes. Tienen ustedes una profesión bendecida.
Saludos desde Barcelona.
¡Muchas gracias Ana Mª! Bienvenida a nuestro espacio.
EliminarSaludos desde La Plata, Argentina.