¿De dónde viene la expresión “el cuadrado de dos es cuatro”?

Veamos…

Si partimos de la sucesión de los números impares

1, 3, 5, 7, 9,…

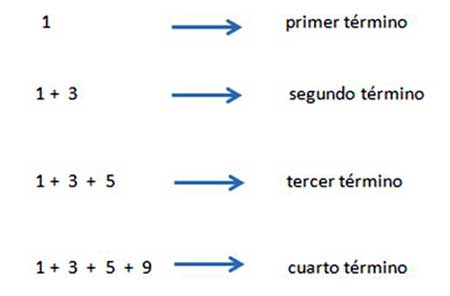
Podemos construir, por sumas, una nueva sucesión cuyos términos serán:

Y así siguiendo…

La sucesión:

1, 4, 9, 16, 25,…

es la obtenida por las sumas de los términos de la sucesión de números impares. Es, en lenguaje de los pitagóricos, la sucesión de los números cuadrados, denominación que marca la forma de la disposición de los redondos.

Los números cuadrados son muy ricos para el análisis. En primer lugar, por ser un símbolo de valor en la aritmo-geometría pitagórica y, en segundo lugar, por ser dignos sobrevivientes de la familia de los números figurados.

Aparecen en la obra euclidiana y “viven” aún entre nosotros. Sin embargo, es necesario no olvidar que, en la aritmética pitagórica, los números cuadrados son números –sumas. En cambio, para Euclides y para nosotros, son productos: resultados de la multiplicación de un número por sí mismo.

Creemos que su permanencia está fundada en el hecho de facilitar el pasaje de llegada hacia el cálculo de áreas.

Para Tales de Mileto… la cuestión primaria no era qué sabemos, sino cómo sabemos. Aristóteles.

Fuente:
Palacios, A. Catarino, G. (2004). Pitágoras de Samos y sus redonditos de Sumota. Buenos Aires: Lumen.