“En el gran templo de Benarés, debajo de la cúpula que marca el centro del mundo, yace una base de bronce, en donde se encuentran acomodadas tres agujas de diamante, cada una del grueso del cuerpo de una abeja y de una altura de 50 cm aproximadamente. En una de estas agujas, Dios, en el momento de la Creación, colocó sesenta y cuatro discos de oro, el mayor sobre la base de bronce y el resto de menor tamaño conforme se va ascendiendo. Día y noche, incesantemente, los sacerdotes del templo se turnan en el trabajo de mover los discos de una aguja a otra de acuerdo con las leyes impuestas e inmutables de Brahma, que requieren que siempre haya algún sacerdote trabajando, que no muevan más de un disco a la vez y que deben colocar cada disco en alguna de las agujas de modo que no cubra a un disco de radio menor. Cuando los sesenta y cuatro discos hayan sido transferidos de la aguja en la que Dios los colocó en el momento de la Creación a otra aguja, el templo y los brahmanes se convertirán en polvo y, junto con ellos, el mundo desaparecerá”
Texto original de Henri de Parville (1884)
El templo de Benarés ya no existe y no hay, por tanto, ningún juego con estas características. Lo increíble de esta leyenda es que tiene miles de años y tiene, aunque no se vean, muchas matemáticas.
Investiga quién fue el dios Brahma.
¿Existe la ciudad de Hanoi?
Tomado de https://rea.ceibal.edu.uy/elp/las_torres_de_hanoi/leyenda.html
No sería novedoso decir que los juegos matemáticos pueden ser usados con amplios beneficios en la formación matemática, en todos los niveles y grados de la enseñanza. El hecho real es que se los usa en forma bastante escasa en todos los medios escolares, en todos los lugares del mundo. Los profesores ven con buenos ojos estas recomendaciones sobre el empleo de los juegos en la enseñanza, pero en la práctica las desechan. La razón es muy simple: por lo común no pueden desprenderse de la idea de que el tiempo destinado a juegos es tiempo robado al programa escolar.
Objetivos.Esa razón, a su vez, depende de otra: no ven de qué manera los diferentes juegos pueden articularse eficazmente en el curriculum de Matemática. Si ambos territorios quedan desconectados, es lógico que el profesor tienda a considerar a los juegos como intrusos o agregados indeseables a su ya recargada tarea escolar.
Lo que se expone a continuación es el conjunto de los resultados que hemos obtenido mediante la utilización sistemática de un entretenimiento de tipo matemático con alumnos de segundo año de una Escuela de Comercio. Como ya lo hemos señalado en otras ocasiones, se trata de un establecimiento oficial, sin características especiales en cuanto al alumnado. La división es una de las cuatro con que cuenta el turno de mañana y está formada por 45 alumnos, de los cuales 26 son niñas y el resto, varones.
El entretenimiento utilizado es un clásico de la recreación matemática, conocido como "La torre de Hanoi". Los resultados obtenidos demuestran que se pueden conseguir altos beneficios en cuanto al desarrollo del pensamiento matemático y la formación general de los alumnos, sin necesidad de alterar la marcha normal de los programas o las planificaciones corrientes. Lo más importante que se puede conseguir es el desarrollo, en los adolescentes, de las formas superiores del pensamiento y el acerca miento a los métodos más amplios y generales de la Matemática.
La torre de Hanoi
Disponemos de tres parantes verticales, en los cuales se colocan discos de cartulina agujereados en el centro, de modo que puedan ser desplaza dos con facilidad en los soportes. Hay —por lo menos en principio— ocho discos, de tamaños crecientes, y están apilados de mayor a menor en una de las columnas. La figura muestra el dispositivo completo.
La tarea propuesta consiste en llevar la columna de uno de los parantes a cualquiera de los otros dos (una restricción del juego puede consistir en trasladarla a uno de los soportes, por ejemplo el último, pero no lo afecta de lleno). Para realizar el traslado, solamente se puede llevar un disco por vez, pero de modo tal que nunca un disco quede colocado sobre otro de tamaño menor. Los discos pueden ser movidos, indistintamente, a uno u otro de los soportes verticales, pero el traslado total debe cumplirse en la menor cantidad posible de movimientos.
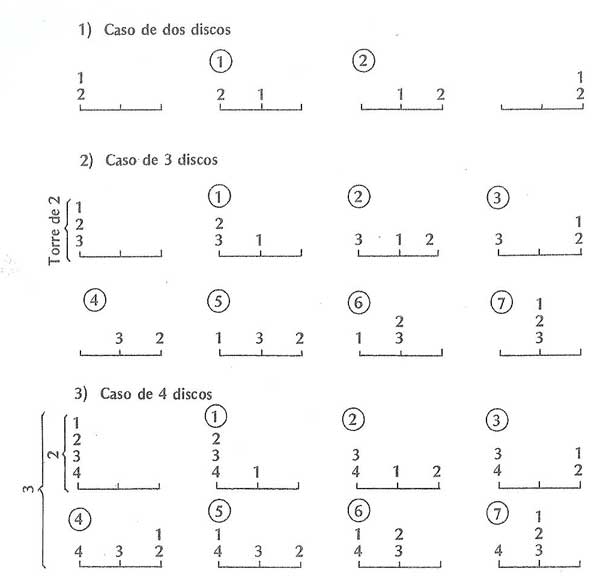
Como medio de simplificación, se puede enfocar el problema por partes, realizando tareas más simples en los primeros intentos. Para esto, se limitan los discos a 2, 3, 4, etc. Puede demostrarse (los adolescentes hallan la fórmula por sí mismos en muchos casos) que el número mínimo de movimientos necesarios está dado por la expresión 2n — 1, donde n es el número de discos. De esta manera se halla que para 2 discos el número mínimo es de 3 movimientos; para 3, de 7; para 4, de 15 y así sucesivamente. Para 8 discos (la cantidad original del entretenimiento) se tiene 21. Son 255 movimientos los necesarios.
Si se procede con orden y método, se halla, en no mucho tiempo, que el secreto necesario para evitar los errores o la repetición indebida de movimientos, es comprender lo que el juego-problema tiene de recursivo, esto es, de repetitivo, porque los pasos dados en el caso de 2 se vuelven a dar en 3, 4, etc.
A continuación, y para guía de los lectores, damos algunos ejemplos de traslados, recalcando, justamente, lo que hay en todos de esquema para los casos siguientes.
Aspectos psicológicos y pedagógicos del problema
Hemos elegido la torre de Hanoi para ser presentada ante un curso de segundo año, como queda dicho. En una experiencia realizada a continuación, se probaron las conclusiones obtenidas con un curso de tercer año de la misma escuela, siempre en condiciones normales de trabajo, e insertando el tema como apéndice o prolongación de las tareas comunes. En todos los casos se dejó en libertad a los alumnos no obligándolos a cumplir con la tarea propuesta pero recompensando con buenas calificaciones a los que se esforzaron en resolver el problema.
La utilización de la torre de Hanoi nos fue sugerida por el empleo que de ella hace Piaget en una de sus experiencias. Esta se encuentra en uno de sus libros más recientes ("La toma de conciencia", Morata, Madrid). Piaget la aplica para verificar una hipótesis con respecto a la forma en que los niños y adolescentes pasan de la acción efectiva a la inteligencia. Esta hipótesis sigue siendo enteramente válida para explicar los comportamientos que exhiben nuestros alumnos, razón por la cual nos ocuparemos con algún detalle de los argumentos que Piaget utiliza y de las experiencias y resultados que expone.
Piaget presenta la torre de Hanoi, con dos únicos discos, a niños de 5 años en adelante. Es notable observar que aún en un problema tan simple en apariencia como es el del traslado de dos discos, los pequeños fracasan o tienen éxito, pero al cabo de múltiples tanteos y errores. Más aún, después de haber tenido éxito, no generalizan lo aprendido ni toman conciencia de las combinaciones que conducen al resulta do buscado. He aquí un problema del mayor interés: los niños aciertan al cabo de numerosas pruebas, pero no comprenden lo que han hecho ni son capaces de explicar los mecanismos que han utilizado, Piaget nos muestra la similitud de este problema con otro que ha estudiado en otros trabajos (transferir el contenido de un vaso a otro mediante la utilización de un intermediario) y lo explica por la falta de un sistema interno que permita la transitividad operatoria (porque en esto consisten los desplazamientos de los discos). Piaget nos dice: "hay en este período un primado sistemático de las acciones exploratorias sobre toda deducción, con falta de toma de conciencia de las acciones exitosas". Podríamos agregar que, tal como se ha expuesto repetidamente, la inteligencia no es sino un conjunto de métodos apropiados que permiten la reducción de la información. En este caso particular, los niños de poca edad tienen al alcance de la mano los resultados correctos y los aplican en el problema, pero carecen de un sistema que les permita ordenar el conjunto de los datos en una totalidad coherente. Por eso son dominados por la variedad de los elementos y pierden las leyes que gobiernan la totalidad.
A partir de los 7-8 años los éxitos con dos discos son inmediatos, pero vuelven los tanteos para tres discos. Es notable comprobar que la acción adelanta siempre a la toma de conciencia y que los éxitos, aún los repetidos, no equivalen a una comprensión de lo realizado. Esto es, por otra parte, enteramente concordante con todo lo que se desprende de las investigaciones de Piaget y confirma lo que sabemos acerca del origen de las operaciones de la inteligencia. Las acciones particulares a que da lugar el problema de la torre de Hanoi dan lugar a coordinaciones más y más generales. Así por ejemplo, la transitividad particular de cada uno de los problemas conduce a la transitivadad lógico-matemática, que no depende de ningún contenido sino que se aplica a cualquier situación de las mismas características. Piaget ha insistido en el hecho de que las estructuras proceden de las acciones del sujeto, pero no solamente de ellas, sino también de reelaboraciones y coordinaciones que no son en modo alguno inmediatas. De otro modo, no se podría entender cómo los éxitos parciales no desembocan en la generalización y la comprensión inmediatas. Saber hacer no es equivalente de saber pensar o de comprender, aunque unas conductas deriven de las otras.
En el estadio que se inicia alrededor de los 11-12 años (los comienzos del pensamiento formal) se obtienen "éxitos estables y rápidos para tres discos y una anticipación más y más inferencial para los números superiores, con una utilización explícita de la experiencia anterior".
Lo que tiene de interesante la torre de Hanoi es que, comenzando por no ser otra cosa que un pasatiempo matemático, un entretenimiento como los hay muchos, acaba por ser la fuente de interesantes cuestiones de tipo general por un lado y el sustrato de un conjunto de acciones que tienden, junto a muchas otras, hacia la elaboración de las estructuras de la inteligencia. Los adolescentes, que hablan con claridad de un "mismo principio" o de un "mismo sistema", comprenden, de acuerdo con la edad y el nivel, lo que hay de general en el problema. Veremos de inmediato cómo una parte nada desdeñable de ellos se acercan, con notable perspicacia, a la formulación de la expresión matemática que lo resume.
Resultados obtenidos
Los alumnos de segundo año tienen, en promedio, 13-14 años. Algunos de ellos, no precisamente todos, han ingresado en el pensamiento formal, mientras que la mayoría se encuentra, de un modo u otro, en camino hacia él. En el curso que hemos indicado obtuvimos, desde un principio, reacciones altamente positivas (recordemos que los chicos fue ron motivados con la idea de recompensas en calificaciones). De todas maneras, el interés legítimo y enteramente autónomo, privó en muchos casos, por ejemplo en la construcción material de la torre, con parantes de madera y discos de cartón prensado.
Con el material, la tarea de realización y de interpretación pudo asumir formas más prácticas. De todas maneras, cabe señalar que la mayor parte de los chicos que produjeron resultados, los obtuvieron por el simple expediente de colocar números encolumnados en hojas de papel. Tal como lo muestran los datos de Piaget, la solución con dos, tres o cuatro elementos resulta fácil e inmediata. Dos niños del curso extienden rápidamente sus acciones exitosas a cantidades mayores (cinco, seis y luego siete) sin mayores problemas. En un caso hay superabundancia de movimientos con respecto a otros, lo que conduce al problema de saber cuál es la mínima cantidad de desplazamientos en cada uno de los casos.
En forma totalmente empírica hallan que existe un número definido de movimientos para cada cantidad de discos, que corresponde a la solución óptima (esto es, con la menor cantidad de desplazamientos). Estos movimientos, como ya hemos visto, son tres para dos discos, siete para tres, quince para cuatro, etc. Es de lo más interesante anotar que varios de los chicos pasaron rápidamente a la solución para cuatro, cinco, seis, y aún siete discos. Recordemos que para siete discos se requieren 127 desplazamientos, lo que da una idea clara de la existencia de un sólido criterio para encarar el conjunto del problema. Es cierto que varias de las soluciones presentan movimientos innecesarios, pero esto no impide considerar la existencia de un sistema de fondo que dirige el conjunto de los desplazamientos.
En exacto acuerdo con lo que Piaget prevé, siempre ocurre que la acción adelanta a la toma de conciencia del problema. En su experiencia Piaget no pide a los niños el descubrimiento de la fórmula 2n — 1 ó la demostración de que es correcta, cosa que nosotros hemos tratado de obtener de nuestros alumnos.
En la búsqueda de la fórmula hemos observado un conjunto de reacciones altamente sugestivas. En el curso de segundo año hallamos adolescentes que buscaban una expresión matemática general por una vía empírica, mediante el análisis de los resultados obtenidos. Encuentran, por ejemplo, que las diferencias entre los valores sucesivos (3; 7; 15; 31; etc.) dan una serie particular. En efecto, la diferencia entre 7 y 3 es 4, la diferencia entre 15 y 7 es 8, entre 31 y 15 es 16. De este modo se obtiene la sucesión 4, 8, 16, 32, etc., en la cual reconocen la multiplicación constante por el factor 2.
Si en este momento se les pide, por ejemplo, cuántos movimientos se requieren para 10 discos, proceden en forma sucesiva y hallan el resulta do pedido. Naturalmente, se quedan detenidos si se les solicita el resultado correspondiente a un número muy grande, como 60 ó cualquier otro.
Es importante hacer notar que estas tareas fueron desarrolladas como complementos de la actividad corriente. Hemos destinado a veces una hora completa a estos ejercicios, pero en la mayor parte de los casos no pasamos de algunos minutos de actividad en una clase. El grupo entero participó, según el nivel de cada alumno. Muchos de ellos no hicieron otra cosa que divertirse un poco con sus propios titubeos o los ajenos en la búsqueda de la solución correcta; los más avanzados llegaron a comprender lo que es esencial en el sistema: su recursividad. En efecto: cuando se pasan dos elementos, quedan libre el tercero, que puede ser desplazado en ese momento a una columna libre. Lógicamente, hay que recomenzar, porque la torre de dos (una "subtorre", si se quiere) debe ser trasladada nuevamente. Cuando se han pasado tres, hay que mover la "subtorre" de tres una vez más, para poder pasar la de cuatro y así sucesivamente.
Hay una manera empírica de obtener la fórmula. Si los chicos escriben la serie 4, 8, 16, 32, 64 y restan la unidad, obtienen los valores pedidos. Esto surge de los números obtenidos. Pero si se tiene en cuenta que acabamos de decir (o, la recursividad o repetición de lo ya realizado en cada nuevo paso) se pasa de la simple constatación a la explicación causal del problema, en cuanto la fórmula deriva de la naturaleza misma de los hechos y no de la regularidad de los datos obtenidos.
Importa mucho decir que los chicos de segundo año son muy rápidos en la solución del problema (no todos, pero sí una buena parte). Los muy buenos pueden, incluso, ganarle al profesor, cosa que se entiende muy claramente pensando en las relaciones entre la acción misma y su toma de conciencia. Por el contrario, les resulta bastante más problemático hallar la ley general. Para obtenerla se apoyan en los datos conseguidos y les cuesta entender y expresar lo que hacen en la práctica con tanta seguridad.
La misma experiencia fue repetida, a continuación, con alumnos de tercer año de la misma escuela, siempre dentro de la enseñanza corriente y como un complemento de ella. Aquí hay diferencias evidentes. Los alumnos de tercer año se desempeñan eficazmente en actos, pero demuestran clarísimos progresos en la conceptualización. Les resulta mucho más fácil obtener y explicar la fórmula general que a los alumnos de segundo año.
Por supuesto, lo volvemos a decir, que existen niveles en el acceso a este problema. Pero éste es, precisamente, uno de los hechos que más nos inclinan a ponderar las virtudes del entretenimiento matemático que recomendamos. Todos los alumnos participan, a ninguno se le escapan los datos del problema; todos pueden resolverlo, por lo menos para una determinada cantidad de discos. Algunos van más lejos, pero el camino no está cerrado para nadie.
Terminaremos diciendo que una consecuencia de lo hecho fue la presentación, por parte de los chicos, de un conjunto de problemas obtenidos de diarios, revistas de entretenimientos, etc., lo que atestigua el interés y el gusto con que encararon esta variante de la actividad corriente.
Tomado de: I.I.E. Revista del Instituto de Investigaciones Educativas. Año 5- N 22.Julio 1979
Durante varios años fue el director de la revista "La Obra", dedicada a la orientación didáctica del magisterio primario. Participó en jornadas y congresos en el país y en el extranjero y fue contratado como asesor de la OEA en Venezuela para un programa de perfeccionamiento de la enseñanza de las ciencias.
Ha publicado numerosos artículos sobre temas didácticos y educativos en general. En 1969 la Biblioteca de Ciencias de la Educación de la Editorial Estrada publicó la versión integral de una experiencia didáctica realizada en el Colegio Nacional "Nicolás Avellaneda", con el título: "La enseñanza de las Ciencias".
Integró el Consejo de Redacción de la Revista del Instituto de Investigaciones Educativas y fue investigador-jefe de este organismo.




Comentarios
Publicar un comentario